题目内容
【题目】如图,∠AOB的内部有一点P,在射线OA,OB边上各取一点P1 , P2 , 使得△PP1P2的周长最小,作出点P1 , P2 , 叙述作图过程(作法),保留作图痕迹. 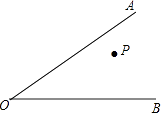
【答案】解:如图,作点P关于直线OA的对称点E,点P关于直线OB的对称点F,连接EF交OA于P1 , 交OB于P2 , 连接PP1 , PP2 , △PP1P2即为所求. 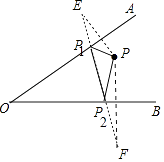
理由:∵P1P=P1E,P2P=P2F,
∴△PP1P2的周长=PP1+P1P2+PP2=EP1+p1p2+p2F=EF,
根据两点之间线段最短,可知此时△PP1P2的周长最短
【解析】作点P关于直线OA的对称点E,点P关于直线OB的对称点F,连接EF交OA于P1 , 交OB于P2 , 连接PP1 , PP2 , △PP1P2即为所求.
【考点精析】利用轴对称-最短路线问题对题目进行判断即可得到答案,需要熟知已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.

练习册系列答案
相关题目
【题目】某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q = W + 100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
次数n | 2 | 1 |
速度x | 40 | 60 |
指数Q | 420 | 100 |
(1)用含x和n的式子表示Q;
(2)当x = 70,Q = 450时,求n的值;
(3)若n = 3,要使Q最大,确定x的值;
(4)设n = 2,x = 40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420,若能,求出m的值;若不能,请说明理由.