Question

如图，已知菱形ABCD，AB＝AC，E、F分别是边BC、AD的中点，连接AE，CF． (1)证明：四边形AECF是矩形； (2)若AB＝8，求菱形的面积．

Answer 1

答案：
解析：

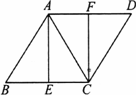
(1)证明：∵四边形ABCD是菱形， 　　∴AB＝BC， 　　又∵AB＝AC， 　　∴△ABC是等边三角形． 　　∵E是边BC的中点， 　　∴AE⊥BC， 　　∴∠AEC＝90°． 　　∵E、F分别是边BC、AD的中点， 　　∴，． 　　又∵四边形ABCD是菱形， 　　∴AD∥BC，AD＝BC， 　　∴AF∥EC，AF＝EC， 　　∴四边形AECF是平行四边形． 　　又∵∠AEC＝90°， 　　∴四边形AECF是矩形． 　　(2)解：在Rt△ABE中，， 　　所以．