题目内容
【题目】已知直线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,
点, ![]() 为
为![]() 的中点,
的中点, ![]() 为射线
为射线![]() 上一点,连
上一点,连![]() ,将
,将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得线段
得线段![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
【答案】![]()
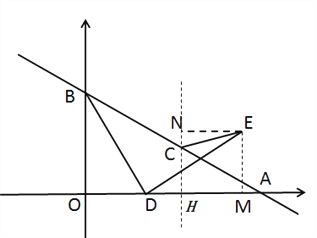
【解析】根据题意,画出图形(如图所示),直线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,
点, ![]() 为
为![]() 的 中点,可得A(4,0),B(0,2),C(2,1),所以OB=2,0A=4.过点E作EM⊥x轴于点M,过点E作NC⊥x轴,过点E作EN⊥NC于点N,因为BD⊥DE,∠BOD=∠AMD=90°,即可证得∠ODB=∠MED,再由BD=DE,根据AAS即可判定△ODB≌△MED,根据全等三角形的对应边相等可得OD=EM,OB=DM=2,设OD=EM=m,则OM=2+m,由点C为AB的中点可得OH=HM=2,即可求得HM=m,所以EN=m.又因C(2,1),EM=NH=m,可得NC=m-1.在Rt△CNE中,根据勾股定理可得
的 中点,可得A(4,0),B(0,2),C(2,1),所以OB=2,0A=4.过点E作EM⊥x轴于点M,过点E作NC⊥x轴,过点E作EN⊥NC于点N,因为BD⊥DE,∠BOD=∠AMD=90°,即可证得∠ODB=∠MED,再由BD=DE,根据AAS即可判定△ODB≌△MED,根据全等三角形的对应边相等可得OD=EM,OB=DM=2,设OD=EM=m,则OM=2+m,由点C为AB的中点可得OH=HM=2,即可求得HM=m,所以EN=m.又因C(2,1),EM=NH=m,可得NC=m-1.在Rt△CNE中,根据勾股定理可得![]() ,当
,当![]() 时,
时, ![]() 最小,最小为
最小,最小为![]() ,所以EC最小为
,所以EC最小为![]() .
.

练习册系列答案
相关题目