��Ŀ����
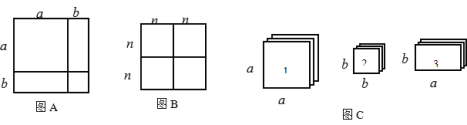
����Ŀ�� ����֪��ijЩ�������ʽ����һЩ��Ƭƴ�ɵ�ͼ����������ͣ����磺ͼA������������![]() ��ʵ��������һЩ��Ƭƴ�ɵ�ͼ�����Ҳ���Զ�ijЩ��������ʽ������ʽ�ֽ�.
��ʵ��������һЩ��Ƭƴ�ɵ�ͼ�����Ҳ���Զ�ijЩ��������ʽ������ʽ�ֽ�.
��1��ͼB���Խ��͵Ĵ������ʽ�� ��
��2�������㹻��������κ;��ο�Ƭ����ͼC��
����Ҫƴ��һ�����Ϊ��3a+b����a+2b���ľ��Σ�����Ҫ1�ſ�Ƭ �ţ�2�ſ�Ƭ �ţ�3�ſ�Ƭ �ţ�
���Ի���һ����������1�ſ�Ƭ��2�ſ�Ƭ��3�ſ�Ƭƴ�ɵľ��Σ�ʹ�þ��ε����Ϊ6a2+7ab+2b2���������㻭��ͼ�������6a2+7ab+2b2������ʽ�ֽ�.
���𰸡���1����2n��2=4n2��2n��2n=4n2����2���� 3��2 ,7���� 6a2+7ab+2b2=��2a+b����3a+2b����ͼ������
��������
��1�����������ε�������������ɽ����
��2���������3a+b����a+2b����ֵ�����ɵó��𰸣�
�ڸ����������жϳ���Ҫ�ֱ���Ҫ����1�š�2�š�3�ŵ�ͼ�Σ�Ȼ��ƴ�ڻ���ͼ�Σ����ɵó��𰸣�����ͼ�κ;��������ʽ�������.
�⣺��(2n)2=4n2��2n��2n=4n2
�Ƣ�![]() ������Ҫ1�ſ�Ƭ3�ţ�2�ſ�Ƭ2�ţ�3�ſ�Ƭ7�ţ�
������Ҫ1�ſ�Ƭ3�ţ�2�ſ�Ƭ2�ţ�3�ſ�Ƭ7�ţ�
�ڸ������⣬��Ҫ6��1��ͼ�Σ���Ҫ2��2��ͼ�Σ���Ҫ7��3��ͼ�Σ�����ƴ�ڣ�����ͼ��һ�����߳��ֱ�Ϊ��2a+b���ͣ�3a+2b���ij����Σ�

6a2+7ab+2b2=��2a+b����3a+2b��