题目内容
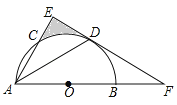
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)
【答案】(1)证明见解析;(2)![]() ﹣6π.
﹣6π.
【解析】试题分析:(1)直接利用切线的判定方法结合圆心角定理分析得出OD⊥EF,即可得出答案;
(2)直接利用得出S△ACD=S△COD,再利用S阴影=S△AED﹣S扇形COD,求出答案.
试题解析:解:(1)连接OD,∵D为![]() 的中点,∴∠CAD=∠BAD,∵OA=OD,∴∠BAD=∠ADO,∴∠CAD=∠ADO,∵DE⊥AC,∴∠E=90°,∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°,∴OD⊥EF,∴EF为半圆O的切线;
的中点,∴∠CAD=∠BAD,∵OA=OD,∴∠BAD=∠ADO,∴∠CAD=∠ADO,∵DE⊥AC,∴∠E=90°,∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°,∴OD⊥EF,∴EF为半圆O的切线;
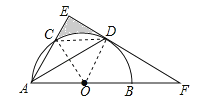
(2)连接OC与CD,∵DA=DF,∴∠BAD=∠F,∴∠BAD=∠F=∠CAD,又∵∠BAD+∠CAD+∠F=90°,∴∠F=30°,∠BAC=60°,∵OC=OA,∴△AOC为等边三角形,∴∠AOC=60°,∠COB=120°,∵OD⊥EF,∠F=30°,∴∠DOF=60°,在Rt△ODF中,DF=![]() ,∴OD=DFtan30°=6,在Rt△AED中,DA=
,∴OD=DFtan30°=6,在Rt△AED中,DA=![]() ,∠CAD=30°,∴DE=DAsin30°=
,∠CAD=30°,∴DE=DAsin30°=![]() ,EA=DAcos30°=9.
,EA=DAcos30°=9.
∵∠COD=180°-∠AOC-∠DOF=60°,由CO=DO,∴△COD是等边三角形,∴∠OCD=60°,∴∠DCO=∠AOC=60°,∴CD∥AB.故S△ACD=S△COD,∴S阴影=S△AED﹣S扇形COD=![]() ×9×
×9×![]() ﹣
﹣![]() =
=![]() ﹣6π.
﹣6π.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案【题目】儿童服装店老板以50元的价格购进20件衣服,针对不同的顾客,20件衣服的售价不完全相同,若以68元为标准,将超出的钱数记为正,不足的钱数记为负,记录结果如下表:
售出件数 | 5 | 4 | 2 | 1 | 7 | 1 |
售价 | +2 | +3 | +1 | 0 | —2 | —1 |
(1)问该服装店售完这20件衣服后,赚了多少钱?
(2)老板为了促销,对购买价格不低于标准的每个顾客送了价值5元的小礼物,如果不考虑其他因素,这20件衣服实际赚了多少?


