题目内容
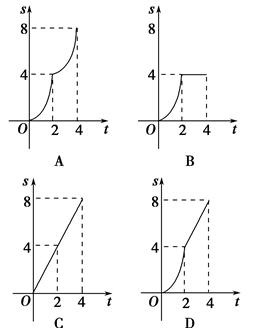
在矩形ABCD中，AB=2
，BC=6，点E为对角线AC的中点，点P在边BC上，连接PE、PA.当点P在BC上运动时，设BP=x，△APE的周长为y，下列图象中，能表示y与x的函数关系的图象大致是（ ）
A．
B.
C．
D．
A.
解析试题分析：应用特殊元素法和排他法解题：
∵在矩形ABCD中，AB=2，BC=6，∴∠ACB=300，∠CAB=600，AC=2AB.
∵点E为对角线AC的中点，∴AB=AE.
当点P在起始位置B时,△APE是等边三角形，∴△APE的周长
.
∵
，∴
.∴可排除选项B.
当△APE周长最小时，如图，作点A关于BC的对称点A1,连接A1E交BC于点P1,则△AP1E周长最小.
∴可排除选项C,D.故选A.
考点：1.动点问题的函数图象分析；2．锐角三角函数定义；3.特殊角的三角函数值；4.实数的大小比较；5.轴对称的应用（最短线路问题）；5．特殊元素法和排他法的应用．
名校课堂系列答案我市某商场有甲、乙两种商品，甲种每件进价15元，售价20元；乙种每件进价35元，售价45元．
（1）若商家同时购进甲、乙两种商品100件，设甲商品购进x件，售完此两种商品总利润为y 元．写出y与x的函数关系式．
（2）该商家计划最多投入3000元用于购进此两种商品共100件，则至少要购进多少件甲种商品？若售完这些商品，商家可获得的最大利润是多少元？
（3）“五•一”期间，商家对甲、乙两种商品进行表中的优惠活动，小王到该商场一次性付款324元购买此类商品，商家可获得的最小利润和最大利润各是多少？
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①4ac﹣b2＜0；②4a+c＜2b；③3b+2c＜0；④m（am+b）+b＜a（m≠﹣1），其中正确结论的个数是（ ）
| A．4个 | B．3个 | C．2个 | D．1个 |
已知点A（
，
）在抛物线
上，则点A关于抛物线对称轴的对称点坐标为
| A．（-3，7） | B．（-1，7） | C．（-4，10） | D．（0，10） |
将二次函数y=x2的图象向右平移1个单位，再向上平移2个单位后，所得图象的函数表达式是
| A．y=(x–1)2+2 | B．y=(x+1)2+2 |
| C．y=(x–1)2–2 | D．y=(x+1)2–2 |
如图，已知点A1，A2，…，A2011在函数
位于第二象限的图象上，点B1，B2，…，B2011在函数位于第一象限的图象上，点C1，C2，…，C2011在y轴的正半轴上，若四边形
、
，…，
都是正方形，则正方形的边长为
| A．2010 | B．2011 | C．2010 | D．2011 |
抛物线y=-x2+2x+3的顶点坐标是( )
| A．(-1，4) | B．(1，3) | C．(-1，3) | D．(1，4) |
