题目内容
在四边形ABCD中,∠A:∠B:∠C:∠D=2:1:2:1,则这个四边形是
- A.等腰梯形
- B.正方形
- C.直角梯形
- D.平行四边形
D
分析:根据四边形的内角和为360度,可求出各角,从而判断它的形状.
解答:四边形的内角和为360度,
∵∠A:∠B:∠C:∠D=2:1:2:1,
∴假设∠A=2x,
∴∠B=x,∠C=2x,∠D=x,
∴2x+x+2x+x=360°,
∴6x=360°,
∴x=60°,
故这个四边形的各角分别为120°、60°、120°、60°,
∴这个四边形是平行四边形.
故选:D.
点评:此题主要考查了四边形的内角和是360度,及平行四边形的判定,熟练掌握平行四边形的判定定理是解决问题的关键.
分析:根据四边形的内角和为360度,可求出各角,从而判断它的形状.
解答:四边形的内角和为360度,
∵∠A:∠B:∠C:∠D=2:1:2:1,
∴假设∠A=2x,
∴∠B=x,∠C=2x,∠D=x,
∴2x+x+2x+x=360°,
∴6x=360°,
∴x=60°,
故这个四边形的各角分别为120°、60°、120°、60°,
∴这个四边形是平行四边形.
故选:D.
点评:此题主要考查了四边形的内角和是360度,及平行四边形的判定,熟练掌握平行四边形的判定定理是解决问题的关键.

练习册系列答案
相关题目
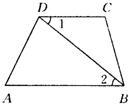 11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=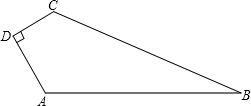
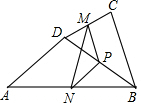 如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?