题目内容
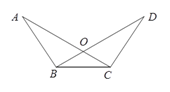
【题目】如图，抛物线
与y轴交于点C，与x轴交于点A和点B．若N点是AC所在直线下方该抛物线上的一个动点，过点N作MN平行于
轴，交AC于点M．
(1) 求直线AC的解析式；
（2）当点N运动至抛物线的顶点时，求此时MN的长；
（3）设点N的横坐标为t，MN的长度为l；
①求l与t之间的函数关系式，并写出t的取值范围；
②l是否存在最值，有如有写出最值；
（4）点D是点B关于轴的对称点．抛物线上是否有点N，使△ODM是等腰三角形？
若存在，请求出此时△CAN的面积；若不存在，请说明理由．
【答案】（1）y=x-4；（2）当t=2时，l有最大值2，此时N（2，2）；（3）存在，点M的坐标为（2，﹣2），（1，-3），
=4或3.
【解析】试题分析：（1）设直线AC的解析式为y=kx+b，过A（4，0）、C（0，-4）两点，即可求得k、b的值，从而求得直线AC的解析式；（2）求得抛物线的顶点坐标及当x=1时点M的坐标，即可求得MN的长；（3）①设
，根据MN=（t-4）-（
），化简即可求得l与t之间的函数关系式，根据图象直接写出x的取值范围即可；②存在，分DO=DM、MO=MD和MO=OD(这种情况不存在)三种情况讨论求解即可，第三种情况不存在，可以不写.
试题解析：
（1）∵抛物线的解析式为：
∴A（4，0）C（0，-4）
∵过A，C两点
∴
（2）∵抛物线的解析式为：
顶点坐标为（1，
）
直线AC的解析式y=x-4,当x=1时，M（1，-3）
∴MN=
（3）①∵
∴
（ 4≤t≤0）
，
∴当t=2时，l有最大值2，此时N（2，2）
（3）存在．
∵点B（-2，0），
∴点D是点B关于y轴的对称点，∴点D（2，0））
在△ODM中，
（ⅰ）若DO=DM，
∵A（4，0），D（2，0），∴AD=OD=DM=2。
又在Rt△AOC中，OA=OC=4，
∴∠OAC=45°。∴∠DMA=∠OAC=45°。
∴∠ADM=90°。此时，点M的坐标为（2，﹣2）。
（ⅱ）若MO=MD，过点M作MH⊥x轴于点H。
由等腰三角形的性质得：OH=OD=1，∴AH=3，
∴在等腰直角△AHM中，HM=AH=3，
∴M（1，-3）
综上所述，使得△ODM是等腰三角形，所求点M的坐标为：（2，﹣2），（1，-3）, △CAN的面积为4或3.
