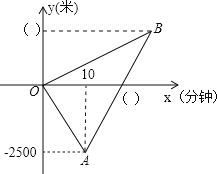
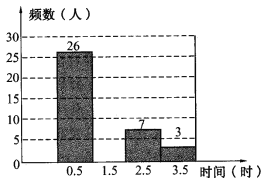
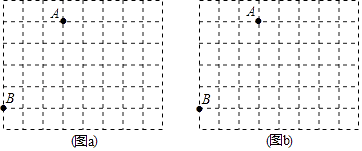
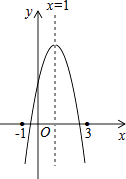ƒøƒ⁄»ð
°æƒø°ø»Ù“ª∏ˆ»˝Œª ˝![]() ∆‰÷–a°¢b°¢c≤ª»´œýµ»«“∂º≤ªŒ™
∆‰÷–a°¢b°¢c≤ª»´œýµ»«“∂º≤ªŒ™![]() £¨÷ÿ–¬≈≈¡–∏˜ ˝Œª…œµƒ ˝◊÷ø…µ√µΩ“ª∏ˆ◊Ó¥Û ˝∫Õ“ª∏ˆ◊Ó–° ˝£¨¥À◊Ó¥Û ˝∫Õ◊Ó–° ˝µƒ≤ÓΩ–◊ˆ‘≠ ˝µƒ≤Ó ˝£¨º«Œ™
£¨÷ÿ–¬≈≈¡–∏˜ ˝Œª…œµƒ ˝◊÷ø…µ√µΩ“ª∏ˆ◊Ó¥Û ˝∫Õ“ª∏ˆ◊Ó–° ˝£¨¥À◊Ó¥Û ˝∫Õ◊Ó–° ˝µƒ≤ÓΩ–◊ˆ‘≠ ˝µƒ≤Ó ˝£¨º«Œ™![]() ¿˝»Á£¨536µƒ≤Ó ˝
¿˝»Á£¨536µƒ≤Ó ˝![]() £Æ
£Æ
£®1£©![]() ______£¨
______£¨![]() ______£Æ
______£Æ
£®2£©»Ù“ª∏ˆ»˝Œª ˝![]() ∆‰÷–
∆‰÷–![]() «“∂º≤ªŒ™
«“∂º≤ªŒ™![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() ƒÐ±ª99’˚≥˝£Æ
ƒÐ±ª99’˚≥˝£Æ
£®3£©»Ùs°¢t «∏˜ ˝Œª…œµƒ ˝◊÷æ˘≤ªŒ™0«“ª•≤ªœýµ»¡Ω∏ˆ»˝Œª◊‘»ª ˝£¨sµƒ∏ˆŒª ˝◊÷Œ™1£¨ ÆŒª ˝◊÷ «∏ˆŒª ˝◊÷µƒ3±∂£¨∞ŸŒª ˝◊÷Œ™x£¨tµƒ∞ŸŒª ˝◊÷Œ™y£¨ ÆŒª ˝◊÷ «∞ŸŒª ˝◊÷µƒ2±∂£¨tµƒ∏ˆŒª ˝◊÷”Îsµƒ∞ŸŒª ˝◊÷œýÕ¨![]() £¨»Ù
£¨»Ù![]() ƒÐ±ª3’˚≥˝£¨
ƒÐ±ª3’˚≥˝£¨![]() ƒÐ±ª11’˚≥˝£¨«Û
ƒÐ±ª11’˚≥˝£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
°æ¥∞∏°ø![]() £¨
£¨![]() £ª
£ª![]() º˚Ω‚Œˆ£ª
º˚Ω‚Œˆ£ª![]() £Æ
£Æ
°æΩ‚Œˆ°ø
![]() ∏˘æð
∏˘æð![]() µƒ∂®“«ÛΩ‚º¥ø…£ª
µƒ∂®“«ÛΩ‚º¥ø…£ª
![]() œ»∏˘æð
œ»∏˘æð![]() µƒ∂®“£¨«Û≥ˆ
µƒ∂®“£¨«Û≥ˆ![]() πÿ”⁄a£¨b£¨cµƒ¥˙ ˝ Ω£¨º¥ø…÷§√˜À¸ƒÐ±ª99’˚≥˝£ª
πÿ”⁄a£¨b£¨cµƒ¥˙ ˝ Ω£¨º¥ø…÷§√˜À¸ƒÐ±ª99’˚≥˝£ª
![]() œ»¡–≥ˆs£¨tµƒ¥˙ ˝ Ω£¨∏˘æð
œ»¡–≥ˆs£¨tµƒ¥˙ ˝ Ω£¨∏˘æð![]() ƒÐ±ª3’˚≥˝£¨
ƒÐ±ª3’˚≥˝£¨![]() ƒÐ±ª11’˚≥˝»∑∂®x£¨yµƒ÷µ£¨‘Ÿ∏˘æð
ƒÐ±ª11’˚≥˝»∑∂®x£¨yµƒ÷µ£¨‘Ÿ∏˘æð![]() µƒ∂®“«ÛΩ‚º¥ø…
µƒ∂®“«ÛΩ‚º¥ø…
![]() £¨
£¨![]() £¨
£¨
π ¥∞∏Œ™£∫396£¨297
![]() «“∂º≤ªŒ™0£¨
«“∂º≤ªŒ™0£¨
![]() £¨
£¨
![]() ƒÐ±ª99’˚≥˝£Æ
ƒÐ±ª99’˚≥˝£Æ
![]() ”…“‚£¨
”…“‚£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨![]() ƒÐ±ª3’˚≥˝£¨
ƒÐ±ª3’˚≥˝£¨
![]() £¨4£¨7
£¨4£¨7
![]() µ±
µ±![]() ±£¨
±£¨![]() £¨
£¨
![]() °¢t «∏˜ ˝Œª…œµƒ ˝◊÷æ˘≤ªŒ™0«“ª•≤ªœýµ»£¨
°¢t «∏˜ ˝Œª…œµƒ ˝◊÷æ˘≤ªŒ™0«“ª•≤ªœýµ»£¨
![]() ≤ª∑˚∫œÃ‚“‚£¨…·»•
≤ª∑˚∫œÃ‚“‚£¨…·»•
![]() µ±
µ±![]() ±£¨
±£¨![]()
![]() £¨
£¨![]() ƒÐ±ª11’˚≥˝£¨
ƒÐ±ª11’˚≥˝£¨
![]() £¨º¥
£¨º¥![]() £¨
£¨
![]() °¢t «∏˜ ˝Œª…œµƒ ˝◊÷æ˘≤ªŒ™0«“ª•≤ªœýµ»£¨
°¢t «∏˜ ˝Œª…œµƒ ˝◊÷æ˘≤ªŒ™0«“ª•≤ªœýµ»£¨
![]() ≤ª∑˚∫œÃ‚“‚£¨…·»•
≤ª∑˚∫œÃ‚“‚£¨…·»•
![]() µ±
µ±![]() ±£¨
±£¨![]()
![]() £¨
£¨![]() ƒÐ±ª11’˚≥˝£¨
ƒÐ±ª11’˚≥˝£¨
![]() £¨º¥
£¨º¥![]() £¨
£¨
![]() £Æ
£Æ

 ∑¢…¢ÀºŒ¨–¬øŒÃ√œµ¡–¥∞∏
∑¢…¢ÀºŒ¨–¬øŒÃ√œµ¡–¥∞∏