题目内容
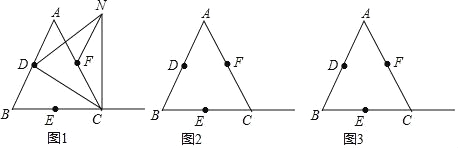
【题目】如图，在△ABC中，∠ACB＝90°，BC＝6，分别以点A和点C为圆心，以相同的长（大于 
AC）为半径作弧，两弧相交于点M和点N ， 作直线MN交AB于点D ， 交AC于点E ， 连接CD ． 则DE的长为 ． 
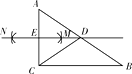
【答案】3
【解析】解：∵DE是AC的垂直平分线，∴AE＝EC ， DE∥BC ， ∠A＝∠DCE ， ∴DE是△ABC的中位线，
∴DE＝
BC=3.
所以答案是3.
【考点精析】掌握三角形的“三线”是解答本题的根本，需要知道1、三角形角平分线的三条角平分线交于一点(交点在三角形内部，是三角形内切圆的圆心，称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部，是三角形的几何中心，称为中心);3、三角形的高线是顶点到对边的距离；注意：三角形的中线和角平分线都在三角形内．
练习册系列答案
快捷英语周周练系列答案
相关题目
【题目】某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核．甲、乙、丙各项得分如下表：
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序．
（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分（不计其他因素条件），请你说明谁将被录用．
