题目内容
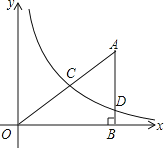
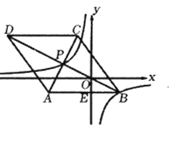
【题目】如图,在平面直角坐标系![]() 中,菱形
中,菱形![]() 的对角线
的对角线![]() 经过原点
经过原点![]() ,与
,与![]() 交于点
交于点![]() 轴于点
轴于点![]() ,点D的坐标
,点D的坐标![]() 为反比例函数
为反比例函数![]() 的图象恰好经过
的图象恰好经过![]() 两点.
两点.
(1)求![]() 的值及
的值及![]() 所在直线的表达式;
所在直线的表达式;
(2)求证:![]() .
.
(3)求![]() 的值.
的值.
【答案】(1)-2,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)根据菱形的性质及反比例函数的对称性可以推出![]() ,再根据点D的坐标即可得到点P的坐标,从而得出k的值;根据点P的坐标可以得出直线
,再根据点D的坐标即可得到点P的坐标,从而得出k的值;根据点P的坐标可以得出直线![]() 的表达式,最后根据OP和AC的关系即可得出直线
的表达式,最后根据OP和AC的关系即可得出直线![]() 的表达式;
的表达式;
(2)由![]() 己等边对等角即可推出
己等边对等角即可推出![]() ;
;
(3)由已知可求得点B的坐标,根据勾股定理可求得OB的值,最后根据同角的余弦即可得出答案.
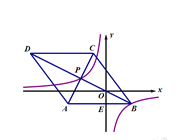
解:(1)∵在菱形![]() 中,对角线
中,对角线![]() 与
与![]() 互相垂直且平分,
互相垂直且平分,
![]() ,
,
![]() 经过原点
经过原点![]() ,且反比例函数
,且反比例函数![]() 的图象恰好经过
的图象恰好经过![]() 两点,
两点,
![]() 由反比例函数
由反比例函数![]() 图象的对称性知:
图象的对称性知:![]() ,
,
![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() ,则
,则![]() ;
;
设直线![]() 的表达式为
的表达式为![]() ,将点
,将点![]() 代入得
代入得![]() ,
,
∴直线![]() 的表达式为
的表达式为![]() ,
,
设直线![]() 的表达式为
的表达式为![]() ,
,
![]() 于点
于点![]() ,
,![]()
将点![]() 及
及![]() ,代入
,代入![]() ,
,
得:![]() ,
,
![]() 直线
直线![]() 的表达式为
的表达式为![]() .
.
(2)证明:由条件得,![]() ,
,
![]() ,
,
![]() ;
;
(3)![]() ,
,
又![]() 与
与![]() 关于原点
关于原点![]() 对称,
对称,
![]()
![]() 在
在![]() 中,
中,![]() ,从而
,从而![]() .
.
则![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目