Question

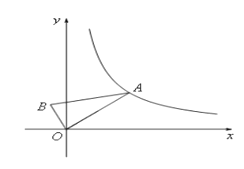
【题目】如图，Rt△OAB的顶点O与坐标原点重合，∠AOB=90°，AO=2BO，当A点在反比例函数 （x>0）的图象上移动时，B点坐标满足的函数解析式为（ ）

A. B.

C. D.

Answer 1

【答案】B

【解析】

过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，设B点坐标满足的函数解析式是 ，易得△AOC∽△OBD，然后由相似三角形面积比等于相似比的平方，求得 ，继而求得答案.

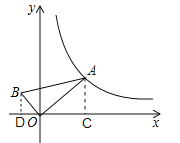
解：如图过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，

设B点坐标满足的函数解析式是

∵∠ACO=∠BDO=90°

∴∠AOC+∠0AC=90°,

∵∠AOB=90°,

∴∠AOC+∠BOD=90°,

∴.∠BOD=∠0AC,

∴△AOC∽△OBD,

∴

∵当A点在反比例函数y=-（x>0）的图象上移动，

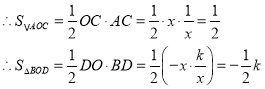
解得：k=

∴B点坐标满足的函数解析式

故答案为：B.