题目内容
【题目】问题探究:
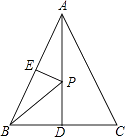
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求出∠AEB的度数以及判断线段CM、AE、BE之间的数量关系,并说明理由.

【答案】探究展示:(1)证明见解析; (2)600.
拓展延伸:(1)∠AEB=900 ;(2)AE= 2CM+BE,理由见解析.
【解析】试题分析:问题探究:(1)先证出∠ACD=∠BCE,那么△ACD≌△BCE,根据全等三角形证出AD=BE;
(2)∠ADC=∠BEC,求出∠ADC=120°,得出∠BEC=120°,从而证出∠AEB=60°;
问题变式:证明△ACD≌△BCE,得出∠ADC=∠BEC、AD=BE,从而得到∠AEB的度数,再由等腰直角三角形的性质得到DM=ME=CM即可.
试题解析:问题探究:
(1) ∵△ACB和△DCE均为等边三角形,∴∠ACB=∠DCE=60°,AC=BC、DC=EC,∴∠ACD=∠BCE,∴△CDA≌△CEB, ∴AD=BE
(2)∵△CDA≌△CEB,∴∠CEB=∠CDA=1200,又∠CED=600,∴∠AEB=1200-600=600.
问题变式:
(1)∵△ACB和△DCE均为等腰直角三角形,∠ACB =∠DCE= 900,
∴AC=BC, CD=CE,
∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD= ∠BCE
∴△ACD≌△BCE
∴AD = BE, ∠BEC=∠ADC=1350.
∴∠AEB=∠BEC-∠CED=1350-450=900
(2)AE= 2CM+BE
在等腰直角三角形DCE中,CM为斜边DE上的高,
∴CM= DM= ME,∴DE=2CM.
∴AE=DE+AD=2CM+BE
∴AE= 2CM+BE

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
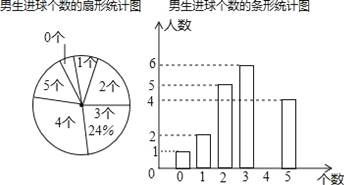
初中学业考试导与练系列答案【题目】为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
女生进球个数的统计表
进球数(个) | 人数 |
0 | 1 |
1 | 2 |
2 | x |
3 | y |
4 | 4 |
5 | 2 |
(1)求这个班级的男生人数;
(2)补全条形统计图,并计算出扇形统计图中进2个球的扇形的圆心角度数;
(3)该校共有学生1880人,请你估计全校进球数不低于3个的学生大约有_____人.