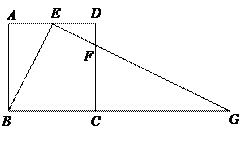题目内容
如图12,△ABC中,∠BAC=90°,AB=AC=1,点D是BC上一个动点(不与B、C重合),在AC上取E点,使∠ADE=45°
(1) 求证:△ABD∽△DCE
(2) 设BD=x,AE=y,求y与x的函数关系式

(1) 求证:△ABD∽△DCE
(2) 设BD=x,AE=y,求y与x的函数关系式

(1)证明:∵∠BAC=90°,AB=AC,∴∠B=∠C=45°
∴∠ADB+∠DAB=135°,∵∠ADE=45°,∴∠ADB+∠EDC=135°
∴∠DAB=∠EDC,∴△ABD∽△DCE
(2)解:∵△ABD∽△DCE,∴ =
=
∴AB=AC=1,∠BAC=90°,
∴BC= ,CD=
,CD= -x,
-x,
∴ =
= ∴CE=
∴CE= x-x2
x-x2
∴AE=AC-CE=1-( x-x2)=x2-
x-x2)=x2- x+1
x+1
即y=x2- x+1(0<x<
x+1(0<x< )
)
∴∠ADB+∠DAB=135°,∵∠ADE=45°,∴∠ADB+∠EDC=135°
∴∠DAB=∠EDC,∴△ABD∽△DCE
(2)解:∵△ABD∽△DCE,∴
 =
=
∴AB=AC=1,∠BAC=90°,
∴BC=
 ,CD=
,CD= -x,
-x,∴
 =
= ∴CE=
∴CE= x-x2
x-x2∴AE=AC-CE=1-(
 x-x2)=x2-
x-x2)=x2- x+1
x+1即y=x2-
 x+1(0<x<
x+1(0<x< )
)略

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 的图象与反比例函数
的图象与反比例函数 的图象交于
的图象交于 两点,与
两点,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,已知
,已知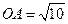 ,
, ,点
,点 的坐标为
的坐标为 .
. ,使得
,使得 与
与 相似,请你求出
相似,请你求出
 ,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2. E、F在边AC、BC上移动时,设
E、F在边AC、BC上移动时,设 ,
, ,
, 关于
关于 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域; 程中,△AED与△CEF能否相似,
程中,△AED与△CEF能否相似,
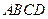 中,
中,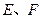 分别是边
分别是边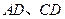 上的点,
上的点,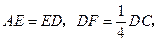 连结
连结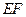 并延长交
并延长交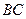 的延长线于点
的延长线于点
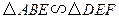 ;
;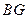 的长.
的长.