Question

【题目】如图，一次函数y1=x+m（m＞0）的图象与x轴交于点A，一次函数y2=nx+2的图象与x轴交于点B，点P（ ）是两函数图象的交点．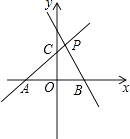

（1）求函数y1、y2的关系式；
（2）若∠PBA=64°，求∠APB的度数；
（3）求四边形PCOB的面积；
（4）在x轴上，是否存在一点Q，使以点Q、B、C为顶点的三角形是等腰三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）解：∵P（ ）是两函数图象的交点，

∴

解得：m=1，n=﹣2，

所以y1=x+1，y2=﹣2x+2；

（2）解：把x=0代入y1=x+1，可得y=1，

把y=0代入y1=x+1，可得x=﹣1，

所以OA=OC=1，

所以∠CAB=45°，

∵∠PBA=64°，

∴∠APB=180°﹣45°﹣64°=71°；

（3）解：∵直线y1=x+1与x，y轴分别交于点A，C，

∴A（﹣1，0），C（0，1），

∴OA=1，OC=1，

∵直线y2=﹣2x+2与x轴交于点B，

∴B（1，0），

∴OB=1，

∴AB=|1﹣（﹣1）|=2，

∴ ；

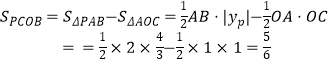（4）解：①当QB=QC时，Q（0，0）；

②当BQ=BC时，点Q（ ，0）或（ ，0）；

③当BC=QC时，Q（﹣1，0）．

【解析】（1）由“点P 是两函数图象的交点”可把P坐标分别代入两解析式中，可求出函数y1、y2的关系式；（2）一次函数y1=x+m的k值为1，可放在RtΔAOC中由OA=OC,求出∠CAB=45°,进而由内角和求出∠APB的度数；（3）不规则四边形面积通常可采用作差法或求和法，本题的S四边形PCOB=SΔPABSΔAOC；（4）出现等腰三角形时，若没指明腰和底，需分类讨论，分别以三个顶点为顶角顶点进行分类，根据等腰三角形的性质得出Q坐标.