题目内容
【题目】显示不全在如图所示的平面直角坐标系中有下面各点:A(0,3),B(1,﹣2),C(3,﹣5),D(﹣3,﹣5),E(3,5),F(5,﹣3),G(4,0).
(1)写出与点C关于坐标轴对称的点;
(2)连接CE,则直线CE与y轴是什么关系(直接写出结论)?
(3)若点P是x轴上的一个动点,连接PD,PF,当PD+PF的值最小时,在图中标出点P的位置,并直接写出P点的坐标.
【答案】
(1)解:点C(3,﹣5)关于x轴对称的点E(3,5),点C(3,﹣5)关于y轴对称的点D(﹣3,﹣5);
(2)解:如图所示:直线CE与y轴平行;
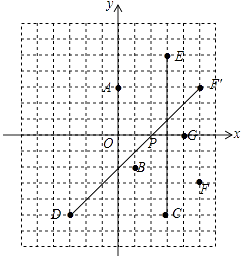
(3)解:作点F关于x轴的对称点F′(5,3),连接DF′交x轴于P,
则DF′的长度即为PD+PF的最小值,
设直线DF′的解析式为:y=kx+b,
∴ ![]() ,
,
∴ ![]() ,
,
∴直线DF′的解析式为:y=x﹣2,
当y=0时,x=2,
∴P点的坐标(2,0).
【解析】(1)关于哪个轴对称,相应坐标不变,另一坐标变为其相反数;(3)动点到两定点距离之和最小问题的解决方法是对称法,作其中一点关于定直线的对称点,连接对称点和另一点,和定直线相交,交点即为最小值位置.
【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识,掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目