��Ŀ����
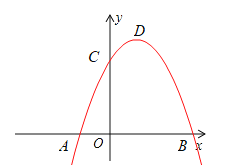
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2+bx+6������A����3��0���͵�B��2��0����ֱ��y��h��hΪ��������0��h��6����BC���ڵ�D����y�ύ�ڵ�E����AC���ڵ�F��
��1���������ߵĽ���ʽ��
��2������AE����hΪ��ֵʱ����AEF��������
��3����֪һ����M����2��0�����ʣ��Ƿ����������ֱ��y��h��ʹ��BDM�ǵ��������Σ������ڣ������h��ֵ�͵�D�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����x2��x+6����2����h��3ʱ����AEF���������������� ![]() ����3�����ڣ���h��
����3�����ڣ���h��![]() ʱ����D������Ϊ��
ʱ����D������Ϊ��![]() ��
��![]() ������h��
������h��![]() ʱ����D������Ϊ��
ʱ����D������Ϊ��![]() ��
��![]() ����
����
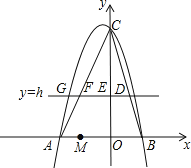
��������
��1�����ô���ϵ�������ɽ�����⣮
��2��������ɵõ�E������Ϊ��0��h������F������Ϊ�� ![]() ��h��������S��AEF��
��h��������S��AEF��![]() OEFE��
OEFE��![]() h
h![]() ����
����![]() ��h��3��2+
��h��3��2+![]() �����ö��κ��������ʼ��ɽ�����⣮
�����ö��κ��������ʼ��ɽ�����⣮
��3�����ڣ��������������Σ��ֱ��г����̼��ɽ�����⣮
�⣺��ͼ��
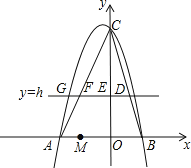
��1����������y��ax2+bx+6������A����3��0���͵�B��2��0����
��![]() ��
��
��ã�![]() ��
��
�������ߵĽ���ʽΪy����x2��x+6��
��2���߰�x��0����y����x2��x+6����y��6��
���C��������0��6����
�辭����A�͵�C��ֱ�ߵĽ���ʽΪy��mx+n����![]() ��
��
��� ![]() ��
��
�ྭ����A�͵�C��ֱ�ߵĽ���ʽΪ��y��2x+6��
�ߵ�E��ֱ��y��h�ϣ�
���E��������0��h����
��OE��h��
�ߵ�F��ֱ��y��h�ϣ�
���F��������Ϊh��
��y��h����y��2x+6����h��2x+6��
���x��![]() ��
��
���F�������� ![]() ��h����
��h����
��EF��![]() ��
��
��S��AEF��![]() OEFE��
OEFE��![]() h
h![]() ����
����![]() ��h��3��2+
��h��3��2+![]() ��
��
�ߩ�![]() ��0��0��h��6��
��0��0��h��6��
�൱h��3ʱ����AEF����������������![]() ��
��
��3�����ڷ��������ֱ��y��h��
��B��2��0����C��0��6����
��ֱ��BC�Ľ���ʽΪy����3x+6����D��m����3m+6����
����BM��BDʱ����m��2��2+����3m+6��2��42��
���m��![]() ��
��![]() ����������
����������
��D��![]() ��
��![]() ������ʱh��
������ʱh��![]() ��
��
����MD��BMʱ����m+2��2+����3m+6��2��42��
���m��![]() ��2����������
��2����������
��D��![]() ��
��![]() ������ʱh��
������ʱh��![]() ��
��
����������������������ֱ��y��![]() ��y��
��y��![]() ��ʹ��BDM�ǵ��������Σ���h��
��ʹ��BDM�ǵ��������Σ���h��![]() ʱ����D������Ϊ��
ʱ����D������Ϊ��![]() ��
��![]() ������h��
������h��![]() ʱ����D������Ϊ��
ʱ����D������Ϊ��![]() ��
��![]() ����
����

����Ŀ��ijУ���꼶ѧ��ij��Ŀѧ�������ɼ����������ҵ����Ԫ��⡢��ĩ��������ɼ����ɵģ����ѧ�������ɼ�80�����ϣ���80�֣���������Ϊ�����������±���С�ź�С����λͬѧ�ijɼ���¼��
�����ҵ | ��Ԫ���� | ��ĩ���� | |
�� | 70 | 90 | 80 |
�� | 60 | 75 | _______ |
���������ҵ����Ԫ��⡢��ĩ��������ɼ���1��2��7��Ȩ����ȷ��ѧ�������ɼ���
��1�������С�ŵ�ѧ�������ɼ�Ϊ���ٷ֣�
��2��С������ĩ����ĩ�ɼ�Ϊ������Ӧ�����ٿ����ٷֲ��ܴﵽ���㣿