题目内容
【题目】在平面直角坐标系中,O为坐标原点,已知A(0,a),B(b,b),C(c,a),其中a,b满足关系式|a-4|+ (b-2)2=0,c=a+b.
(1)求A、B、C三点的坐标,并在坐标系中画出△ABC;
(2)如果在第四象限内有一点P(2,m),请用含m的代数式表示三角形CPO的面积.
【答案】(1)A(0,4),B(2,2),C(6,4),画图见解析;
(2)三角形CPO的面积为4-3m.
【解析】试题分析:(1)根据非负数的性质得到a-4=0,b-2=0,解得a=4,b=2,则c=6,则可写出求A、B、C三点的坐标,然后坐标系中描出3个点;(2)利用分割法求三角形CPO的面积,即用一个矩形的面积分别减去3个三角形的面积.
试题解析:(1)|a-4|+ (b-2)2=0,c=a+b,得a=4,b=2,c=6
∴A、B、C三点的坐标分别为A(0,4),B(2,2),C(6,4)
画图:
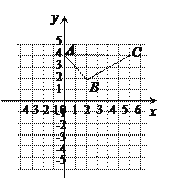 ;
;
(2)如图,三角形CPO的面积=长方形面积-三个三角形面积
=![]()
=![]()

练习册系列答案
相关题目