题目内容
【题目】(1)阅读材料:
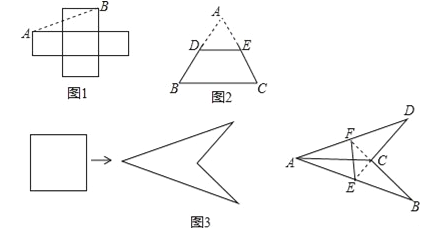
教材中的问题,如图1,把5个边长为1的小正方形组成的十字形纸板剪开,使剪成的若干块能够拼成一个大正方形,小明的思考:因为剪拼前后的图形面积相等,且5个小正方形的总面积为5,所以拼成的大正方形边长为 ,故沿虚线AB剪开可拼成大正方形的一边,请在图1中用虚线补全剪拼示意图.
(2)类比解决:
如图2,已知边长为2的正三角形纸板ABC,沿中位线DE剪掉△ADE,请把纸板剩下的部分DBCE剪开,使剪成的若干块能够拼成一个新的正三角形.
①拼成的正三角形边长为 ;
②在图2中用虚线画出一种剪拼示意图.
(3)灵活运用:
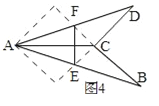
如图3,把一边长为60cm的正方形彩纸剪开,用剪成的若干块拼成一个轴对称的风筝,其中∠BCD=90°,延长DC、BC分别与AB、AD交于点E、F,点E、F分别为AB、AD的中点,在线段AC和EF处用轻质钢丝做成十字形风筝龙骨,在图3的正方形中画出一种剪拼示意图,并求出相应轻质钢丝的总长度.(说明:题中的拼接都是不重叠无缝隙无剩余)
【答案】(1)![]() ;(2)①
;(2)①![]() ;②答案见解析;(3)
;②答案见解析;(3)![]() .
.
【解析】
试题分析:(1)依题意补全图形如图1,利用剪拼前后的图形面积相等,得出大正方形的面积即可;
(2)①先求出梯形EDBC的面积,利用剪拼前后的图形面积相等,结合等边三角形的面积公式即可;
②依题意补全图形如图3所示;
(3)依题意补全图形如图4,根据剪拼的特点,得出AC是正方形的对角线,点E,F是正方形两邻边的中点,构成等腰直角三角形,即可.
试题解析:(1)补全图形如图1所示,由剪拼可知,5个小正方形的面积之和等于拼成的一个大正方形的面积,∵5个小正方形的总面积为5,∴大正方形的面积为5,∴大正方形的边长为![]() ,故答案为:
,故答案为:![]() ;
;
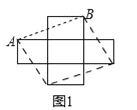
(2)①如图2,∵边长为2的正三角形纸板ABC,沿中位线DE剪掉△ADE,∴DE=![]() BC=1,BD=CE=1
BC=1,BD=CE=1
过点D作DM⊥BC,∵∠DBM=60°,∴DM=![]() ,∴S梯形EDBC=
,∴S梯形EDBC=![]() (DE+BC)×DM=
(DE+BC)×DM=![]() (1+2)×
(1+2)×![]() =
=![]() ,由剪拼可知,梯形EDBC的面积等于新拼成的等边三角形的面积,设新等边三角形的边长为a,∴
,由剪拼可知,梯形EDBC的面积等于新拼成的等边三角形的面积,设新等边三角形的边长为a,∴![]() =
=![]() ,∴a=
,∴a=![]() 或a=﹣
或a=﹣![]() (舍),∴新等边三角形的边长为
(舍),∴新等边三角形的边长为![]() ,故答案为:
,故答案为:![]() ;
;
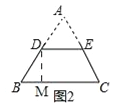
②剪拼示意图如图3所示:
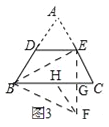
(3)剪拼示意图如图4所示,∵正方形的边长为60cm,由剪拼可知,AC是正方形的对角线,∴AC=![]() cm,由剪拼可知,点E,F分别是正方形的两邻边的中点,∴CE=CF=30cm,∵∠ECF=90°,根据勾股定理得,EF=
cm,由剪拼可知,点E,F分别是正方形的两邻边的中点,∴CE=CF=30cm,∵∠ECF=90°,根据勾股定理得,EF=![]() cm;
cm;
∴轻质钢丝的总长度为AC+EF=![]() +
+![]() =
=![]() cm.
cm.

 阅读快车系列答案
阅读快车系列答案