题目内容
如图,把一个边长为2![]() 的正方形ABCD放在平面直角坐标系中,点A在坐标原点,点C在y轴的正半轴上,经过B、C、D三点的抛物线c1交x轴于点M、N(M在N的左边).
的正方形ABCD放在平面直角坐标系中,点A在坐标原点,点C在y轴的正半轴上,经过B、C、D三点的抛物线c1交x轴于点M、N(M在N的左边).
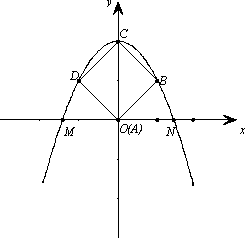
(1)求抛物线c1的解析式及点M、N的坐标;
(2)如下图,另一个边长为2![]() 的正方形
的正方形![]() 的中心G在点M上,
的中心G在点M上,![]() 、
、![]() 在x轴的负半轴上(
在x轴的负半轴上(![]() 在
在![]() 的左边),点
的左边),点![]() 在第三象限,当点G沿着抛物线c1从点M移到点N,正方形
在第三象限,当点G沿着抛物线c1从点M移到点N,正方形![]() 随之移动,移动中
随之移动,移动中![]()
![]() 始终与x轴平行.
始终与x轴平行.
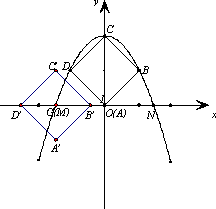
①直接写出点C’、D’移动路线形成的抛物线C(C’)、C(D’)的函数关系式;
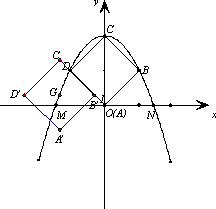
②如图,当正方形![]() 第一次移动到与正方形ABCD有一边在同一直线上时,求点G的坐标.
第一次移动到与正方形ABCD有一边在同一直线上时,求点G的坐标.
答案:
解析:
解析:
|
解:(1)y=- ① ②G(1- |

练习册系列答案
相关题目
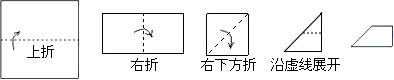
如图,把一个边长为1的正方形经过三次对折后沿中位线(虚线)剪下,则右图展开得到的图形的面积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|

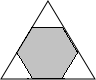 (2005•遵义)如图,把一个边长为6cm的正三角形剪成一个最大的正六边形,则这个正六边形的周长为
(2005•遵义)如图,把一个边长为6cm的正三角形剪成一个最大的正六边形,则这个正六边形的周长为