题目内容
如图,P1、P2、P3…Pn(n为正整数)分别是反比例函数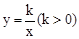 在第一象限图象上的点,A1、A2、A3…An分别为x轴上的点,且△P1OA1、△P2A1A2、△P3A2A3…△PnAn-1An均为等边三角形.若点A1的坐标为(2,0),则点A2的坐标为__________________,点An的坐标为__________________.
在第一象限图象上的点,A1、A2、A3…An分别为x轴上的点,且△P1OA1、△P2A1A2、△P3A2A3…△PnAn-1An均为等边三角形.若点A1的坐标为(2,0),则点A2的坐标为__________________,点An的坐标为__________________.
( ,0);(
,0);(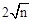 ,0).
,0).
解析试题分析:如图,作P1B⊥x轴于B,P2C⊥x轴于C,P3D⊥x轴于D,
∵△P1OA1为等边三角形,A1(2,0),∴OB=1,P1B=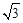 OB=
OB=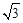 .∴P1的坐标为(1,
.∴P1的坐标为(1,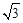 ).
).
∴k=1×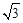 =
=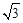 .
.
设A1C=t,
∵△P2A1A2为等边三角形,∴P2C=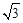 A1C=
A1C=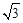 t. ∴P2点的坐标为
t. ∴P2点的坐标为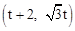 .
.
∴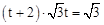 ,解得
,解得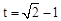 或
或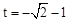 (舍去).
(舍去).
∴A1A2=2t=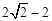 .∴OA2=
.∴OA2= .
.
∴A2点的坐标为( ,0).
,0).
同理得到A3点的坐标为(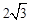 ,0).
,0).
∴An点的坐标为(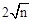 ,0).
,0).
考点:1.探索规律题(图形的变化类);2.反比例函数图象上点的坐标特征;3.等边三角形的性质.

练习册系列答案
相关题目
 上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是
上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是




 的图象在第 象限.
的图象在第 象限. (k>0)的图象上,则y1 y2(填“>”“<”或“=”)
(k>0)的图象上,则y1 y2(填“>”“<”或“=”) ABCD的顶点A、B的坐标分别是A(-1,0)B(0,-2),顶点C、D在双曲线
ABCD的顶点A、B的坐标分别是A(-1,0)B(0,-2),顶点C、D在双曲线 上,边AD交y轴于点E,且
上,边AD交y轴于点E,且
 经过点(-1,2),那么k的值等于 .
经过点(-1,2),那么k的值等于 . 的图象上有三个点为(x1,y1)、(x2,y2)、(x3,y3),若y1<0<y2<y3,则x1,x2,x3的大小关系是 .
的图象上有三个点为(x1,y1)、(x2,y2)、(x3,y3),若y1<0<y2<y3,则x1,x2,x3的大小关系是 . (k≠0)的图象上,点Q(2,4)与点P关于y轴对称,则反比例函数的表达式为________________
(k≠0)的图象上,点Q(2,4)与点P关于y轴对称,则反比例函数的表达式为________________