题目内容
在四边形ABCD中,对角线AC平分∠DAB.
(1)如图①,当∠DAB=120°,∠B=∠D=90°时,求证:AB+AD=AC.
(2)如图②,当∠DAB=120°,∠B与∠D互补时,线段AB、AD、AC有怎样的数量关系?写出你的猜想,并给予证明.
(3)如图③,当∠DAB=90°,∠B与∠D互补时,线段AB、AD、AC还![]() 有上面的数量关系吗?说明理由。
有上面的数量关系吗?说明理由。

解:(1)在四边形ABCD中,∵AC平分∠DAB,∠DAB=120°,
∴∠CAB=∠CAD=60°.又∵∠B=∠D=90°,
∴∠ACB=∠ACD=30°.![]() ,即AB+AD=AC.
,即AB+AD=AC.
(2)AB+AD=AC.
证明如下:如图①,过C点分别作AD和AB延长线的垂线段,垂足分别为E、F.
∵AC平分∠DAB,
∴CE=CF.
∵∠ABC+∠D=180°,
∠ABC+∠CBF=180°,
∴∠CBF=∠D.
又∵∠CED=∠CFB=90°,
∴△CED≌△CFB.∴ED=BF.
∴AD+AB=AE+ED+![]() AB=AE+BF+AB=AE+AF.
AB=AE+BF+AB=AE+AF.
由(1)知AE+AF=A![]() C.
C.
∴AB+AD=AC.
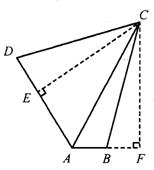
第26题答图①

第26题答图②
(3)AB+AD=![]() AC.
AC.
证明如下:如图②,过C点分别作AB和AD延长线的垂线段,垂足分别是E、F.
∵AC平分∠DAB,∴CE=CF.
∵∠ABC+∠ADC=180°,
∠ADC+∠FDC=180°,
∴∠ABC=∠FDC.
又∵∠CEB=∠CFD=90°.
∴△CEB≌△CFD.∴CB=CD.
延长AB至G,使BG=AD,连结CG.
∵∠ABC+∠ADC=180°,∠ABC+∠CBG=180°,
∴∠CBG=∠ADC.∴△GBC![]() ≌△ADC.
≌△ADC.
∴∠G=∠DAC=∠CAB=45°.∴∠ACG=90°.
![]() .
.
![]() .
.

练习册系列答案
相关题目
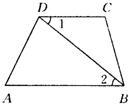 11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
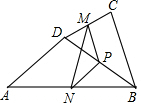 如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?