Question

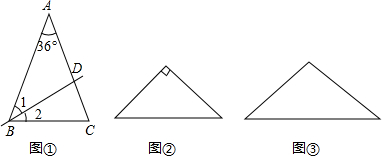
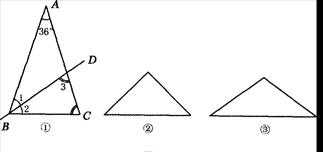
25、数学课上，同学们探究下列命题的准确性：
（1）顶角为36°的等腰三角形具有一种特性，即经过它的某一顶点的一条射线可把它分成两个小等腰三角形．为此，请你解答：如图，已知在△ABC中，AB=AC，∠A=36°，射线BD平分∠ABC交AC于点D．
求证：△DAB与△BCD都是等腰三角形；
（2）在证明了该命题后，有同学发现：下面两个等腰三角形也具有这种特性．请你在下列两个三角形中分别画出一条射线，把它们分别分成两个小等腰三角形，并在图中标出所画小等腰三角形两个底角的度数；
（3）接着，同学们又发现：还有一些既不是等腰三角形也不是直角三角形的三角形也具有这种特性，请你画出两个具有这种特性的三角形示意图（要求两三角形不相似，而且既不是等腰三角形也不是直角三角形，并标出每一个小等腰三角形各内角的度数）．

Answer 1

分析：（1）可以先计算出∠ABC和∠C的度数为（180°-36°）÷2=72°，再求出∠DBA和∠DBC的度数72°÷2=36°；
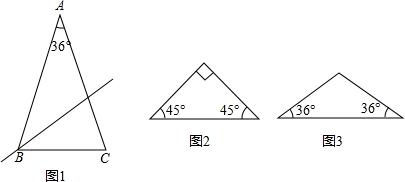
（2）图1根据顶角的度数180°-2×45°=90°，分解成两个角都是45°，图2中一个与底角36°相等、另一个180°-36°×3=72°再作为底角；
（3）先作一个等腰三角形，然后在这个三角形的基础上作出另一个等腰三角形．

解答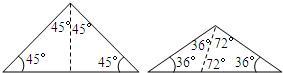：证明：（1）∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
∵射线BD平分∠ABC，
∴∠ABD=∠CBD=36°．
∴∠BDC=72°，
∴AD=BD=BC．
∴△DAB与△BCD都是等腰三角形．（4分）

（2）图1中将顶角90°平分，图2中将顶角108°分解成36°和72°两个角；

（3）如图（符合即可）（5分）

点评：答对本题，需要对等腰三角形的性质和判定比较熟悉．