题目内容
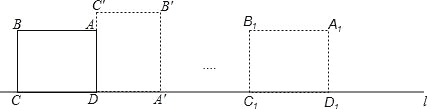
【题目】如图，矩形ABCD中，AB=8，BC=6，边CD在直线l上，将矩形ABCD沿直线l作无滑动翻滚，当点A第一次翻滚到点A1位置时，则点A经过的路线长为 ．
【答案】12π.
【解析】
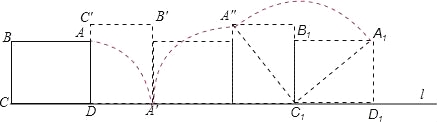
试题分析：如图根据旋转的性质知，点A经过的路线长是三段：①以90°为圆心角，AD长为半径的扇形的弧长；②以90°为圆心角，AB长为半径的扇形的弧长；③90°为圆心角，矩形ABCD对角线长为半径的扇形的弧长．∵四边形ABCD是矩形，AB=8，BC=6，∴BC=AD=3，∠ADC=90°，对角线AC（BD）=10．∵根据旋转的性质知，∠ADA′=90°，AD=A′D=BC=6，∴点A第一次翻滚到点A′位置时，则点A′经过的路线长为：
=3π．同理，点A′第一次翻滚到点A″位置时，则点A′经过的路线长为：
=4π．点A″第一次翻滚到点
位置时，则点A″经过的路线长为：
=5π．则当点A第一次翻滚到点位置时，则点A经过的路线长为：3π+4π+5π=12π．
故答案是：12π．
练习册系列答案
相关题目
