题目内容
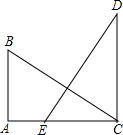 如图,BA∥CD,∠A=90°,AB=CE,BC=ED,则△CED≌________,根据是________.
如图,BA∥CD,∠A=90°,AB=CE,BC=ED,则△CED≌________,根据是________.
△ABC HL
分析:根据两直线平行,同旁内角互补求出∠DCE=90°,然后利用“HL”证明△CED和△ABC全等.
解答:∵BA∥CD,∠A=90°,
∴∠DCE=180°-∠A=180°-90°=90°,
∵在Rt△CED和Rt△ABC中,
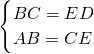 ,
,
∴△CED≌△ABC(HL).
故答案为:△ABC,HL.
点评:本题考查了全等三角形的判定,平行线的性质,求出∠DCE=90°是解题的关键.
分析:根据两直线平行,同旁内角互补求出∠DCE=90°,然后利用“HL”证明△CED和△ABC全等.
解答:∵BA∥CD,∠A=90°,
∴∠DCE=180°-∠A=180°-90°=90°,
∵在Rt△CED和Rt△ABC中,
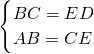 ,
,∴△CED≌△ABC(HL).
故答案为:△ABC,HL.
点评:本题考查了全等三角形的判定,平行线的性质,求出∠DCE=90°是解题的关键.

练习册系列答案
相关题目
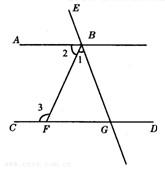 21、如图,AB∥CD,∠1:∠2:∠3=1:2:3,说明BA平分∠EBF的道理.
21、如图,AB∥CD,∠1:∠2:∠3=1:2:3,说明BA平分∠EBF的道理.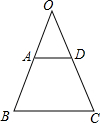 已知:如图,BA与CD相交于O,OA=OD,AD∥BC.求证:AB=CD.
已知:如图,BA与CD相交于O,OA=OD,AD∥BC.求证:AB=CD.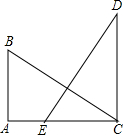 如图,BA∥CD,∠A=90°,AB=CE,BC=ED,则△CED≌
如图,BA∥CD,∠A=90°,AB=CE,BC=ED,则△CED≌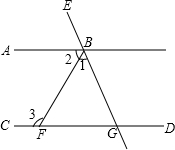 如图,AB∥CD,∠1:∠2:∠3=1:2:3,说明BA平分∠EBF的道理.
如图,AB∥CD,∠1:∠2:∠3=1:2:3,说明BA平分∠EBF的道理.