题目内容
【题目】如图，AC⊥BC，DC⊥EC，AC=BC,DC=EC,若AC=3，CE=4，则AD2+BE2=__________．
【答案】50
【解析】
由△ACE≌△BCD（SAS），推出AE⊥BD，再利用勾股定理即可解决问题．
解：设AC交BD于点J．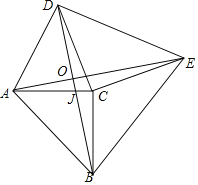
∵AC⊥BC，DC⊥EC，
∴∠ACB=∠DCE=90°，
∴∠ACE=∠DCB，
∵AC=BC，DC=EC，
∴△ACE≌△BCD（SAS），
∴∠CAE=∠CBD，
∵∠CBJ+∠BJC=90°，∠BJC=∠AJO，
∴∠JAO+∠AJO=90°，
∴∠AOJ=90°，
∴AE⊥BD，
∵AC=3，EC=4，
∴AB2=32+32=18，DE2=CD2+CE2=32，
∴AD2+BE2=OD2+OA2+OE2+OB2=（OD2+OE2）+（OA2+OB2）=18+32=50．
故答案为：50．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
【题目】二次函数
，
，
是常数，且
中的
与
的部分对应值如下表所示，则下列结论中，正确的个数有（ ）
|
|
|
|
|
|
|
|
|
|
；
当
时，
；
当
时，的值随值的增大而减小；
方程
有两个不相等的实数根．
A. 4个 B. 3个 C. 2个 D. 1个
