题目内容
【题目】如图,矩形ABCD中,对角线AC的垂直平分线交AD、BC于点E、F,AC与EF交于点O,连结AF、CE. 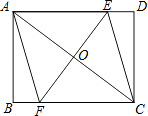
(1)求证:四边形AFCE是菱形;
(2)若AB=3,AD=4,求菱形AFCE的边长.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠EAO=∠FCO,
∵EF是AC的垂直平分线,
∴AO=CO,∠EOA=∠FOC=90°,
在△AEO和△CFO中, 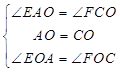 ,
,
∴△AEO≌△CFO(ASA),
∴AE=CF,
∴四边形AFCE是平行四边形,
又∵AC⊥EF,
∴四边形AFCE是菱形
(2)解:∵四边形AFCE是菱形,
∴AF=CF,
设AF=CF=x,则BF=4﹣x,
在Rt△ABF中,AF2=AB2+BF2,
即x2=32+(4﹣x)2,
解得 x= ![]() ,
,
∴菱形AFCE的边长为 ![]()
【解析】(1)由矩形的性质得出AD∥BC,∠EAO=∠FCO,证明△AEO≌△CFO,得出AE=CF,证出四边形AFCE是平行四边形,再由对角线AC⊥EF,即可得出结论;(2)设AF=CF=x,则BF=4﹣x,在Rt△ABF中,根据勾股定理得出方程,解方程即可.
【考点精析】本题主要考查了线段垂直平分线的性质和勾股定理的概念的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

【题目】小东根据学习函数的经验,对函数y= ![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题: 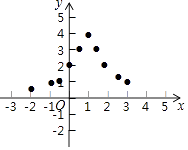
(1)函数y= ![]() 的自变量x的取值范围是
的自变量x的取值范围是
(2)表格是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | ﹣ | 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数y= ![]() 的大致图象;
的大致图象;
(4)结合函数图象,请写出函数y= ![]() 的一条性质:
的一条性质:
(5)如果方程 ![]() =a有2个解,那么a的取值范围是
=a有2个解,那么a的取值范围是