Question

【题目】如图，在平面直角坐标系中，点O为坐标原点．已知反比例函数的图象经A（﹣2，m），过点作AB⊥x轴．垂足为点B，且△OAB的面积为1．

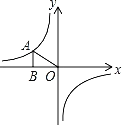
（1）求k和m的值；

（2）点C（x，y）在反比例的图象上，当1≤x≤3时，求函数值y的取值范围．

Answer 1

【答案】（1）m＝1，k＝﹣2；（2）﹣2≤y≤﹣．

【解析】

（1）根据三角形的面积公式先得到m的值，然后把点A的坐标代入，可求出k的值；

（2）先分别求出x=1和3时，y的值，再根据反比例函数的性质求解．

解：（1）∵A（﹣2，m），

∴OB＝2，AB＝m，

∴S△AOB＝OBAB＝×2×m＝1，

∴m＝1；

∴点A的坐标为（﹣2，1），

把A（﹣2，1）代入，

得k＝﹣2×1＝﹣2；

（2）∵反比例函数为，

∴当x＝1时，y＝﹣2；当x＝3时，y＝﹣，

又∵反比例函数位于第二、四象限

∴在x＞0时，y随x的增大而增大，

∴当1≤x≤3时，y的取值范围为﹣2≤y≤﹣．