题目内容
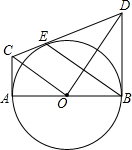 如图,已知AB是⊙O的直径,CA,DB分别与⊙O相切于点A,B,E为上⊙O的一点,连接CE并延长交BD于点D,连接OC,BE,OC∥BE.若AB=3,AC=1,BD=
如图,已知AB是⊙O的直径,CA,DB分别与⊙O相切于点A,B,E为上⊙O的一点,连接CE并延长交BD于点D,连接OC,BE,OC∥BE.若AB=3,AC=1,BD=| 9 | 4 |
(1)求OC与OD的长分别是多少?
(2)求证:CD是⊙O切线;
(3)求证:△COD是直角三角形.
分析:(1)CA,DB分别与⊙O相切于点A,B,得出△CAO和△BOD为直角三角形,利用勾股定理求得OC与OD的长;
(2)连接OE,结合OC∥BE,找出条件证得△CAO≌△CEO,就可以得出结论;
(3)由(2)CD是⊙O切线,利用切线长定理得出CD的长,利用勾股定理的逆定理求证结论成立.
(2)连接OE,结合OC∥BE,找出条件证得△CAO≌△CEO,就可以得出结论;
(3)由(2)CD是⊙O切线,利用切线长定理得出CD的长,利用勾股定理的逆定理求证结论成立.
解答:(1)解:∵CA,DB分别与⊙O相切于点A,B,
∴∠CAO=∠BOD=90°,
∴△CAO和△BOD为直角三角形;
又OA=OB=
AB=
,
则OC=
=
=
;
OD=
=
=
;
(2)证明:
如图,
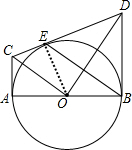
连接OE,则OE=OB,
∴∠OBE=∠OEB,
∵OC∥BE,
∴∠OBE=∠AOC,∠OEB=∠EOC,
∴∠AOC=∠EOC,
又∵OA=OE,OC=OC,
∴△CAO≌△CEO,
∴∠OEC=∠OAC=90°,
∴CD是⊙O切线;
(3)证明:
∵CA,DB分别与⊙O相切于点A,B;CD是⊙O切线;
∴CE=CA=1,DE=DB=
,
∴CD=CE+DE=
;
∵OC2=
,OD2=
,CD2=
,
OC2+OD2=CD2,
∴△COD是直角三角形.
∴∠CAO=∠BOD=90°,
∴△CAO和△BOD为直角三角形;
又OA=OB=
| 1 |
| 2 |
| 3 |
| 2 |
则OC=
| OA2+AC2 |
(
|
| ||
| 2 |
OD=
| OB2+BD2 |
(
|
3
| ||
| 4 |
(2)证明:
如图,

连接OE,则OE=OB,
∴∠OBE=∠OEB,
∵OC∥BE,
∴∠OBE=∠AOC,∠OEB=∠EOC,
∴∠AOC=∠EOC,
又∵OA=OE,OC=OC,
∴△CAO≌△CEO,
∴∠OEC=∠OAC=90°,
∴CD是⊙O切线;
(3)证明:
∵CA,DB分别与⊙O相切于点A,B;CD是⊙O切线;
∴CE=CA=1,DE=DB=
| 9 |
| 4 |
∴CD=CE+DE=
| 13 |
| 4 |
∵OC2=
| 13 |
| 4 |
| 117 |
| 16 |
| 169 |
| 16 |
OC2+OD2=CD2,
∴△COD是直角三角形.
点评:此题考查切线的判定与性质、切线长定理、勾股定理以及勾股定理逆定理、三角形全等的判定与性质等知识点.

练习册系列答案
相关题目
 如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10.
如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10. 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F. (2013•泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是
(2013•泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是
 如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.
如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC. 如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.
如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.