题目内容
如图,直角梯形ABCD中,AD∥BC,∠A=90°,AB=AD=6,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连接EF.
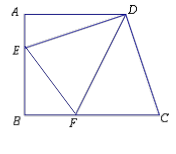
(1) 证明:EF=CF;
(2) 当AE=2时,求EF的长.

(1) 证明:EF=CF;
(2) 当AE=2时,求EF的长.
(1)见解析, (2)EF = 5
解:(1) 如图,过D作DG⊥BC于G
由已知可得四边形ABGD为正方形
∵DE⊥DC
∴∠ADE+∠EDG=90°=∠GDC+∠EDG
∴∠ADE=∠GDC
在△ADE与△GDC中,
∴△ADE≌△GDC (ASA) ···························· 3分
∴DE=DC且AE=GC
在△EDF和△CDF中
∴△EDF≌△CDF(SAS)··························· ·6分
∴EF=CF··································· 7分
(2) ∵AE=2
设EF=x,则BF=8-CF=8-x,BE=4
由勾股定理x2= +42
+42
解得
∴EF = 5 12分
(1)过D作DG⊥BC于G,可得四边形ABGD为正方形,求得△ADE≌△GDC (ASA),△EDF≌△CDF(SAS),从而得出结论
(2)利用勾股定理求解
由已知可得四边形ABGD为正方形
∵DE⊥DC
∴∠ADE+∠EDG=90°=∠GDC+∠EDG
∴∠ADE=∠GDC
在△ADE与△GDC中,

∴△ADE≌△GDC (ASA) ···························· 3分
∴DE=DC且AE=GC
在△EDF和△CDF中

∴△EDF≌△CDF(SAS)··························· ·6分
∴EF=CF··································· 7分
(2) ∵AE=2
设EF=x,则BF=8-CF=8-x,BE=4
由勾股定理x2=
 +42
+42解得

∴EF = 5 12分
(1)过D作DG⊥BC于G,可得四边形ABGD为正方形,求得△ADE≌△GDC (ASA),△EDF≌△CDF(SAS),从而得出结论
(2)利用勾股定理求解

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 △ADC除外);
△ADC除外);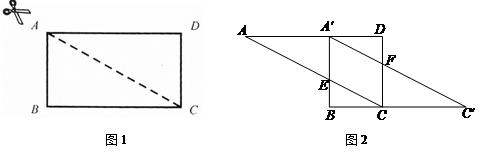
 沿
沿 对折,若
对折,若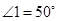 ,则
,则 等于( )
等于( )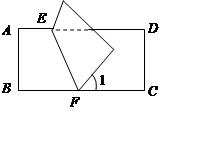







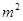 ,
,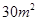 ,
,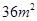 ,则种植白色花卉土地的面积为 m2.
,则种植白色花卉土地的面积为 m2.