题目内容
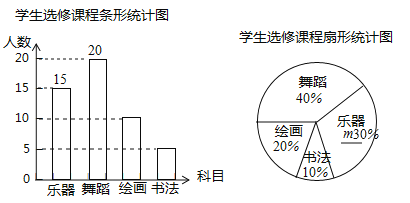
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
【答案】(1)50,30%;(2)作图见解析;(3)![]() .
.
【解析】
试题分析:(1)由舞蹈的人数除以占的百分比求出调查学生总数,确定出扇形统计图中m的值;
(2)求出绘画与书法的学生数,补全条形统计图即可;
(3)列表得出所有等可能的情况数,找出恰好为一男一女的情况数,即可求出所求概率.
试题解析:(1)20÷40%=50(人),15÷50=30%;
故答案为:50;30%;
(2)50×20%=10(人),50×10%=5(人),如图所示:
(3)∵5﹣2=3(名),∴选修书法的5名同学中,有3名男同学,2名女同学,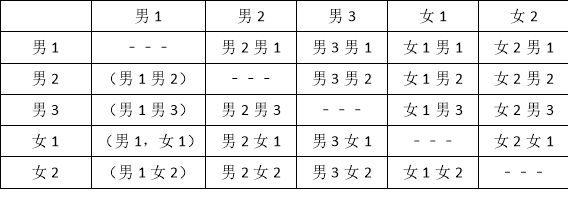
所有等可能的情况有20种,其中抽取的2名同学恰好是1名男同学和1名女同学的情况有12种,则P(一男一女)=![]() =
=![]() .
.

练习册系列答案
相关题目