��Ŀ����
����Ŀ��������ԭ��ΪԲ�ģ�1Ϊ�뾶��Բ�ֱ�x��y����������ڵ�A��B��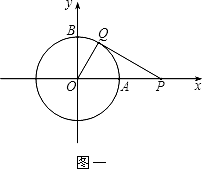
��1����ͼһ������P�ӵ�A����������x�����������˶������ͬʱ������Q�ӵ�B����������Բ�ܰ�˳ʱ�뷽�������˶�������Q���˶��ٶȱȵ�P���˶��ٶ���������1����P�˶����㣨2��0������ʱPQǡ���ǡ�O�����ߣ�����OQ�����QOP�Ĵ�С��
��2������Q���գ�1���еķ�����ٶȼ����˶�����Pͣ���ڵ㣨2��0�������������Q�پ���5���ֱ��PQ����O�صõ��ҳ���
���𰸡�
��1���⣺��ͼһ������AQ��
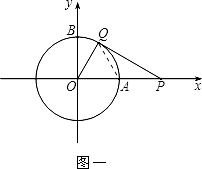
�������֪��OQ=OA=1��
��OP=2��
��AΪOP���е㣮
��PQ���O�����ڵ�Q��
���OQPΪֱ�������Σ�
�� ![]() ��
��
����OAQΪ�ȱ������Σ�
���QOP=60�㣮
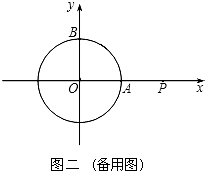
��2���⣺�ɣ�1����֪��Q�˶�1��ʱ�����Ļ������Ե�Բ�Ľ�Ϊ30�㣬��Q���գ�1���еķ�����ٶȼ����˶�����ô�ٹ�5�룬��Q�����ڡ�O��y�Ḻ����Ľ��㴦����ͼ��������ֱ��PQ���O������һ������ΪD��
��O��OC��QD�ڵ�C����CΪQD���е㣮
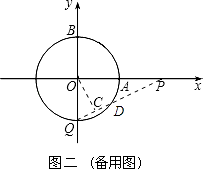
�ߡ�QOP=90�㣬OQ=1��OP=2��
��QP= ![]() ��
��
�� ![]() ��
��
��OC= ![]() =
= ![]() ��
��
��OC��QD��OQ=1��OC= ![]() ��
��
��QC= ![]() =
= ![]() ��
��
��QD= ![]() ��
��
����������1�������������ʶ������Լ�OQ��OP֮��Ĺ�ϵ���ɵó���QOP�Ķ�������2�����ݴ������������ɶ���������⼴��.
�����㾫����������Ĺؼ���������ɶ����ĸ�������֪ʶ������ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2���Լ������ߵ����ʶ��������⣬�˽����ߵ����ʣ�1�������е㴹ֱ�������뾶��ֱ����Բ������2�������е㴹ֱ�����ߵ�ֱ�߱ؾ���Բ��3��Բ�����ߴ�ֱ�ھ����е�İ뾶��

 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�