题目内容
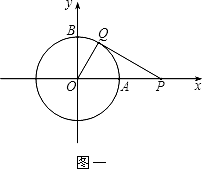
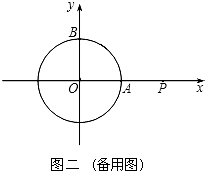
【题目】如图,点A是反比例函数y= ![]() (x>0)上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比例函数图象上移动时,点B也在某一反比例函数y=
(x>0)上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比例函数图象上移动时,点B也在某一反比例函数y= ![]() 图象上移动,则k的值为( )
图象上移动,则k的值为( )
A.﹣4
B.4
C.﹣2
D.2
【答案】A
【解析】∵点A是反比例函数y= ![]() (x>0)上的一个动点,
(x>0)上的一个动点,

∴可设A(x, ![]() ),
),
∴OC=x,AC= ![]() ,
,
∵OB⊥OA,
∴∠BOD+∠AOC=∠AOC+∠OAC=90°,
∴∠BOD=∠OAC,且∠BDO=∠ACO,
∴△AOC∽△OBD,
∵OB=2OA,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴OD=2AC= ![]() ,BD=2OC=2x,
,BD=2OC=2x,
∴B(﹣ ![]() ,2x),
,2x),
∵点B反比例函数y= ![]() 图象上,
图象上,
∴k=﹣ ![]() 2x=﹣4,
2x=﹣4,
所以答案是:A.

练习册系列答案
相关题目