题目内容
【题目】如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
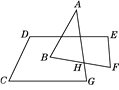
【答案】540°.
【解析】试题分析:连接GF,根据三角形的内角和定理可得∠A+∠B+∠AHB=180°,∠HFG+∠HGF+∠GHF=180°,根据对顶角相等可得∠AHB=∠GHF,所以∠A+∠B=∠HFG+∠HGF,所以∠A+∠B+∠C+∠D+∠E+∠F+∠G=∠C+∠D+∠E+∠EFH+∠HFG+∠HGC+∠HGF,根据五边形的内角和公式即可求解.
试题解析:
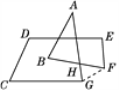
如图,连接GF.
∵∠A+∠B+∠AHB=180°,∠HFG+∠HGF+∠GHF=180°,∠AHB=∠GHF,
∴∠A+∠B=∠HFG+∠HGF.
∵∠C+∠D+∠E+∠EFG+∠FGC=540°,∠EFG=∠EFH+∠HFG,∠FGC=∠HGC+∠HGF,
∴∠C+∠D+∠E+∠EFH+∠HFG+∠HGC+∠HGF=540°,
∴∠A+∠B+∠C+∠D+∠E+∠EFH+∠HGC=540°.

练习册系列答案
相关题目