题目内容
【题目】如图1,在△ABC中,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B,C在AE的异侧,BD⊥AE于D,CE⊥AE于E.

(1)△ABD与△CAE全等吗?BD与DE+CE相等吗?请说明理由。
(2)如图2,若直线AE绕点A旋转到图②所示的位置(BD<CE)时,其余条件不变,则BD与DE、CE的关系如何?请说明理由
(3)如图3,若直线AE绕点A旋转到图③所示的位置(BD>CE)时,其余条件不变,则BD与DE、CE的关系如何?
(4)根据以上的讨论,请用简洁的语言表达BD与DE、CE的数量关系.
【答案】(1)见解析;(2)BD=DE-CE,理由见解析; (3)BD=DE-CE;理由见解析;(4) 当点B、C在AE异侧时,BD=DE+CE;当点B、C在AE同侧时,BD=DE-CE.
【解析】
(1)在直角三角形中,由题中条件可得∠ABD=EAC,又有AB=AC,则有一个角及斜边相等,则可判定Rt△BAD≌Rt△AEC,由三角形全等可得三角形对应边相等,进而通过线段之间的转化,可得出结论;
(2)由题中条件同样可得出Rt△BAD≌Rt△AEC,得出对应线段相等,进而可得线段之间的关系;
(3)同(2)的方法即可得出结论.
(4)利用(1)(2)(3)即可得出结论.
(1)证明:在△ABD和△CAE中,
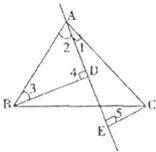
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
又∠4=∠5=90°,AB=AC,
∴△ABD≌△CAE.(AAS),
∴BD=AE,AD=CE.
又AE=AD+DE,
∴AE=DE+CE,
即BD=DE+CE.
(2)BD=DE-CE.
证明:∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
又∵BD⊥DE,∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE.
又AB=AC,∠ADB=∠CEA=90°,
∴△ADB≌△CEA.
∴BD=AE,AD=CE.
∵DE=AD+AE,
∴DE=CE+BD,
即BD=DE-CE.
(3)同(2)的方法可证:BD=DE-CE.
(4)当点B、C在AE异侧时,BD=DE+CE;当点B、C在AE同侧时,BD=DE-CE.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案