题目内容
有若干个数,第一个为a1,第二个为a2,第三个为a3…,第n个为an…,若a1=
,从第二个数起,每个数都等于“1与它前面那个数的差的倒数.”
(1)试计算:a2=
;
(2)请你根据以上结果写出a2010=
,a2012=
| 1 |
| 2 |
(1)试计算:a2=
2
2
,a3=-1
-1
,a4=| 1 |
| 2 |
| 1 |
| 2 |
(2)请你根据以上结果写出a2010=
-1
-1
,a2011=| 1 |
| 2 |
| 1 |
| 2 |
2
2
.分析:(1)根据1与它前面那个数的差的倒数,即an+1=
,即可求解;
(2)根据(1)的计算,得到结果出现的规律,即可确定.
| 1 |
| 1+an |
(2)根据(1)的计算,得到结果出现的规律,即可确定.
解答:解:(1)a2=
=2,a3=
=-1,a4=
=
;
(2)根据(1)的计算可以得到a1=a4,则这些数三个数循环一次,
2010÷3=670,则a2010=a3=-1,a2011=a1=
,a2012=a2=2.
故答案是:(1)2,-1,
;(2)-1,
,2.
| 1 | ||
1-
|
| 1 |
| 1-2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
(2)根据(1)的计算可以得到a1=a4,则这些数三个数循环一次,
2010÷3=670,则a2010=a3=-1,a2011=a1=
| 1 |
| 2 |
故答案是:(1)2,-1,
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了有理数的运算,正确理解结果的循环的规律是关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
图1是由若干个小圆圈堆成的一个图案,最上面一层有2个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.完成下列问题:
(1)每一层的圆圈个数与层数的关系为:
| 层数 | 1 | 2 | 3 | … | n |
| 每层圆圈个数 | … |
将图1倒置后与原图1拼成图2的形状,则图2中每层圆圈个数为________;n层圆圈总数为________;由于图2中圆圈个数是图1中的________倍,可以得出图1中所有圆圈的个数为________.
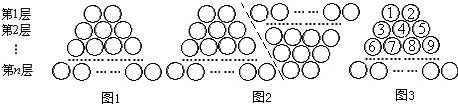
(3)假设图1中的圆圈共有10层,我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层从左边数第三个圆圈中的数是________.

 ,从第二个数起,每个数都等于“1与它前面那个数的差的倒数.”
,从第二个数起,每个数都等于“1与它前面那个数的差的倒数.”