题目内容
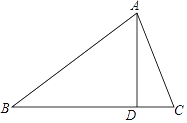
【题目】已知在△ABC中,AB=AC。

(1)若D为AC的中点,BD把三角形的周长分为24cm和30cm两部分,求△ABC三边的长;
(2)若D为AC上一点,试说明AC>![]() (BD+DC)。
(BD+DC)。
【答案】(1)三角形的三边长为16,16,22或20,20,14;(2)理由见解析
【解析】试题分析:(1)分两种情况讨论:当AB+AD=30,BC+DC=24或AB+AD=24,BC+DC=30,所以根据等腰三角形的两腰相等和中线的性质可求得,三边长为16,16,22或20,20,14;
(2)根据三角形两边之和大于第三边即可得到AC>![]() (BD+DC).
(BD+DC).
试题解析:
(1)设三角形的腰AB=AC=x,
若AB+AD=24cm,
则:x+x=24
∴x=16
三角形的周长为24+30=54cm
所以三边长分别为16,16,22;
若AB+AD=30cm,
则:x+x=30
∴x=20
∵三角形的周长为24+30=54cm
∴三边长分别为20,20,14;
因此,三角形的三边长为16,16,22或20,20,14。
(2)∵AC=AD+CD,AB=AC,
∴2AC=AB+AD+CD>BD+DC,
∴AC>![]() (BD+DC)。
(BD+DC)。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目