Question

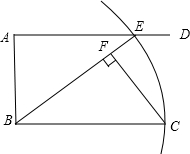如图，AD∥BC，∠BAD=90°，以点B为圆心，BC长为半径画弧，与射线AD相交于点E，连接BE，过C点作CF⊥BE，垂足为F．若AB=2，BC=3，则BF的长为________．

Answer 1

分析：由题意得BC=BE=3，在Rt△AEB中，可求出sin∠AEB，继而可得出sin∠EBC的值，根据CF=BCsin∠EBC可得出CF的长，然后在Rt△BCF中，利用勾股定理可得出BF的长．
解答：由题意得，BC=BE=3，
则∠AEB==，
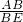∵∠AEB=∠EBC，
∴sin∠EBC=，
∴CF=BCsin∠EBC=2，
在Rt△BFC中，BF==．
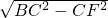故答案为：．
点评：本题考查了勾股定理的知识，注意三角函数在解直角三角形中的应用，难度一般，关键是求出sin∠EBC的值．