题目内容
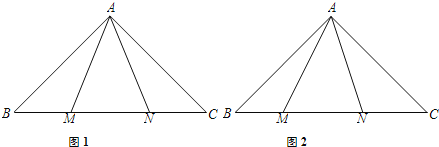
【题目】已知:如图1,在Rt△ABC和Rt△A'B'C'中,AB=A'B',AC=A'C',C=∠C'=90°.
求证:Rt△ABC和Rt△A'B'C'全等.
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)将△ABC和△A'B'C'拼在一起,请你画出两种拼接图形;例如图2:(即使点A与点A'重合,点C与点C'重合.)
(3)请你选择你拼成的其中一种图形,证明该命题.

【答案】(1)见解析;(2)见解析;(3)证明见解析.
【解析】
(1)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等;
(2)使点A与点A'重合,点B与点B'重合;使点A与点B'重合,点B与点A'重合;
(3)在(2)的图①中,连接CC',根据等腰三角形的判定与性质,通过“边边边”证明△ABC≌△A'B'C'即可.
(1)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等;
(2)如图:

图①使点A与点A'重合,点B与点B'重合;
图②使点A与点B'重合,点B与点A'重合;
(3)在图①中,∵点A和点A'重合,点B和点B'重合,连接CC'.
∵AC=A'C',
∴∠ACC'=∠AC'C,
∵∠ACB=∠A'C'B'=90°,
∴∠ACB-∠ACC'=∠A'C'B'-∠AC'C,
即∠BCC'=∠BC'C,
∴BC=B'C',
在Rt△ABC和Rt△A'B'C'中,
 ,
,
∴△ABC≌△A'B'C'(SSS).

 阅读快车系列答案
阅读快车系列答案【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
| td style="width:28.95pt; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">m |
|
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .