��Ŀ����
����Ŀ��ij�߿Ƽ���չ��˾Ͷ��500��Ԫ���ɹ����Ƴ�һ���г��������ϴ�ĸ߿Ƽ������Ʒ����Ͷ���ʽ�1500��Ԫ����������������֪����ÿ����Ʒ�ijɱ�Ϊ40Ԫ�������۹����з��֣������۵��۶�Ϊ100Ԫʱ����������Ϊ20��������۵���ÿ����10Ԫ����������������1����������۵���Ϊx��Ԫ������������Ϊy�����������һ��������������=�����۶�����ɱ���Ͷ�ʣ�Ϊz����Ԫ��
��1����д��y��x֮��ĺ�����ϵʽ������д��x��ȡֵ��Χ��
��2����д����һ�������z��x֮��ĺ�����ϵʽ������д��x��ȡֵ��Χ��
��3����˵����һ�깫˾��ӯ�����ǿ��������ӯ�����������Сʱ�IJ�Ʒ�ۼ�
��4����˾�ƻ����ڵ�һ�갴��������ȷ�������۵��ۣ��������ۣ��ڶ��������������1130��Ԫ��������������Ĵ���ͼ��˵�����ڶ�������۵���x��Ԫ��Ӧȷ����ʲô��Χ��
���𰸡���1��y=��![]() x+30����2��
x+30����2��![]() ����3����һ�깫˾�����ˣ�����Ʒ�ۼ۶�Ϊ170Ԫ/��ʱ��������С����С����Ϊ310��Ԫ����4����120��x��220ʱ��������1130�����Եڶ�������۵���Ӧȷ���ڲ�����120Ԫ�Ҳ�����220Ԫ�ķ�Χ��
����3����һ�깫˾�����ˣ�����Ʒ�ۼ۶�Ϊ170Ԫ/��ʱ��������С����С����Ϊ310��Ԫ����4����120��x��220ʱ��������1130�����Եڶ�������۵���Ӧȷ���ڲ�����120Ԫ�Ҳ�����220Ԫ�ķ�Χ��
��������
��1������������۵��۶�λxԪʱ��������������![]() �����Ȼ��ݴ˽�һ�������ϵʽ���ɣ�
�����Ȼ��ݴ˽�һ�������ϵʽ���ɣ�
��2�����������=�����۶�����ɱ���Ͷ���г�������ϵʽ��һ�����ɣ�
��3���ԣ�2���еĹ�ϵʽ������ʽ�ֽ⣬Ȼ���һ����⼴�ɣ�
��4���ڣ�3���Ļ����϶Եڶ�������������г���ϵʽ��Ȼ��ó�ͼ���һ����⼴��.
��1��������ã������۵��۶�λxԪʱ��������������![]() �����
�����
��![]() ==��
==��![]() x+30��
x+30��
��y��x֮��ĺ�����ϵʽ�ǣ�y=��![]() x+30��
x+30��
��2��������ã�![]() ��
��
��z��x֮��ĺ�����ϵʽΪ��![]() ��
��
��3���ɣ�2���ã�![]() ��
��
����![]() ��
��
��![]() �����һ������ˣ�
�����һ������ˣ�
��![]() ʱ��
ʱ��![]() ȡ�����ֵ�����ֵΪ
ȡ�����ֵ�����ֵΪ![]() ��Ԫ��
��Ԫ��
���һ�깫˾�����ˣ�����Ʒ�ۼ۶�Ϊ170Ԫ/��ʱ��������С����С����Ϊ310��Ԫ
��4�����ڶ�������۵��۶�ΪxԪʱ��
�����![]() ��
��
��![]() ʱ��
ʱ��
�����ã�![]() ��
��
��ã�![]() ��
��![]() ��
��
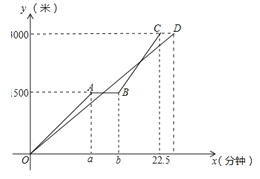
�ຯ����ͼ�������ͼ��ʾ��
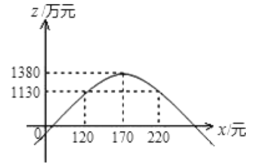
��ͼ����Կ�������120��x��220ʱ��������1130��
��ڶ�������۵���Ӧȷ���ڲ�����120Ԫ�Ҳ�����220Ԫ�ķ�Χ�ڣ�

 �������ϵ�д�
�������ϵ�д�