Question

【题目】已知抛物线C：y＝(x＋2)[t(x＋1)－(x＋3)]，其中－7≤t≤－2，且无论t 取任何符合条件的实数，点A，P 都在抛物线C 上.

（1）当t＝－5时，求抛物线C 的对称轴；

（2）当－60≤n≤－30 时，判断点（1，n）是否在抛物线C上， 并说明理由；

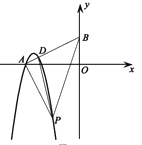
（3）如图，若点A在x轴上，过点A作线段AP的垂线交y轴于点B，交抛物线C于点D，当点D的纵坐标为m＋时，求S△PAD的最小值.

Answer 1

【答案】（1）当t＝－5时，求抛物线C 的对称轴为x＝－

（2）当－60≤n＜－54时，点（1，n）不在抛物线C上，当－54≤n≤－30时，点（1，n）在抛物线C上，理由见解析；

（3）S△PAD的最小值为

【解析】试题分析：(1)把t＝5代入y＝(x＋2)[t(x＋1)－(x＋3)],求出函数解析式,在根据对称轴x=－计算得出;(2) 假设（1，n）在抛物线上，将点（1，n）代入解析式，得n＝6t－12,在根据－7≤t≤－2, 得出当－60≤n＜－54时，点（1，n）不在抛物线C上； 当－54≤n≤－30时，点（1，n）在抛物线C上;(3) 根据点A是抛物线与x轴的交点, 点P在抛物线C 上, 求出A（－2，0），P（－1，－2）, 过点P作PN⊥x轴于点N，证△PAN≌△ABO, 得到BO＝1, PA＝AB＝,过点D作DM⊥x轴于点M，证△DAM∽△BAO,得S△PAD＝,当m取最小值－时， S△PAD的最小值为．

试题解析：

（1）当t＝5时，y＝－6x2－20x－16，

∵－＝－，

∴对称轴为x＝－．

（2）若（1，n）在抛物线上，

将点（1，n）代入解析式，得

n＝6t－12．

∵ －7≤t≤－2，

∴ －54≤n≤－24．

∵ －60≤n≤－30，

∴ 当－60≤n＜－54时，点（1，n）不在抛物线C上；

当－54≤n≤－30时，点（1，n）在抛物线C上.

（3）由题得A（－2，0），P（－1，－2）．

过点P作PN⊥x轴于点N，可得

PN＝AO＝2，∠PNA＝∠AOB＝90°．

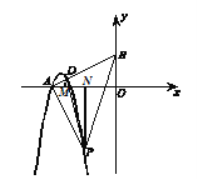
∵ PA⊥AB，

∴ ∠PAN＋∠BAO＝90°．

又∵ ∠ABO＋∠BAO＝90°，

∴ ∠PAN＝∠ABO．

∴ △PAN≌△ABO．

∴ BO＝1，

PA＝AB＝．

过点D作DM⊥x轴于点M，可得

∠DMA＝∠BOA＝90°．

又∵ ∠DAM＝∠BAO，

∴ △DAM∽△BAO．

∴ ．

∴ AD＝．

∴ S△PAD＝APAD＝．

∵ A（－2，0），B（0，1），

∴ 直线AB的解析式为y＝x＋1．

当y＝m＋时，x＝2m－1．

把点D（2m－1，m＋）代入抛物线C的解析式，得t＝1＋ ．

∵ －7≤t≤－2，

∴ －≤m≤－．

∴ m＋＞0．

∴ S△PAD＝ (m＋ )．

∵ ＞0，

∴ S△PAD随m的增大而增大．

∴ 当m取最小值－时， S△PAD的最小值为．

点睛:以二次函数为背景的几何图形变换问题,其核心思想方法主要有分类讨论思想,函数与方程思想,树形结合思想,转化思想,待定系数法,配方法等,要用运动和变化的眼光去观察,研究图形,抓住其中的等量关系和变量关系,综合分析问题 和解决问题的能力.