题目内容
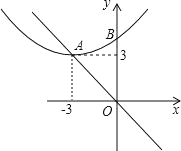
【题目】如图，抛物线y＝ax2+bx+c的顶点为A（﹣3，3），且与y轴交于点B（0，5），若平移该抛物线，使其顶点A沿y＝﹣x由（﹣3，3）移动到（2，﹣2），此时抛物线与y轴交于点B′，则BB′的长度为________．
【答案】6
【解析】
先运用待定系数法求出原抛物线的解析式，再根据平移不改变二次项系数，得出平移后的抛物线解析式，求出B′的坐标，进而得出BB′的长度．
抛物线y=ax2+bx+c顶点为A（-3，3），
∴y=a（x+3）2+3，
∵与y轴交于点B（0，5），
∴5=a（0+3）2+3，
解得：a=
，
∴顶点为A（-3，3）的抛物线为y=（x+3）2+3，
顶点A沿y=-x由（-3，3）移动到（2，-2）的抛物线为y=（x-2）2-2，
即y=x2-
x-
，
得点B′（0，-），BB′的长度为5+=6．
故答案为：6．
练习册系列答案
53天天练系列答案
相关题目
