题目内容
【题目】《九章算术》是我国古代数学名著，书中有下列问题：“今有勾五步，股十二步，问勾中容方几何？”其意思为“今有直角三角形，勾(短直角边)长为5步，股(长直角边)长为12步，问该直角三角形能容纳的正方形边长最大是多少步？”该问题的答案是________步．
【答案】
【解析】
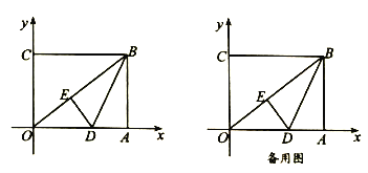
如图1，根据正方形的性质得：DE∥BC，则△ADE∽△ACB，列比例式可得结论；如图2，同理可得正方形的边长，比较可得最大值．
解：如图1，
∵四边形CDEF是正方形，
∴CD=ED，DE∥CF，
设ED=x，则CD=x，AD=12-x，
∵DE∥CF，
∴∠ADE=∠C，∠AED=∠B，
∴△ADE∽△ACB，
∴
＝
，
∴
＝
，
x=，
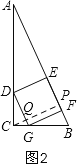
如图2，四边形DGFE是正方形，
过C作CP⊥AB于P，交DG于Q，
设ED=x，
S△ABC=
ACBC=ABCP，
12×5=13CP，
CP=
，
同理得：△CDG∽△CAB，
∴
＝
，
∴
＝
，
x=
＜，
∴该直角三角形能容纳的正方形边长最大是（步），
故答案为：．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
