Question

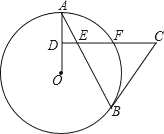
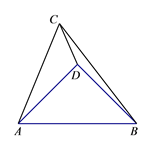
【题目】如图，D为△ABC内一点，且AD =BD，若∠ACD=∠DAB=45°，AC=5，则S△ABC=_______．

Answer 1

【答案】

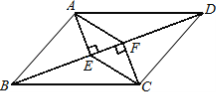
【解析】分析：过D作FD⊥CD交AC于F，连接BF．可证△ADC≌△BDF，得到∠ACD=∠BFD=45°，AC=BF，由∠CFD=45°，得到∠BFC=90°，由S△ABC=ACBF即可得到结论．

详解：过D作FD⊥CD交AC于F，连接BF．

∵∠ACD=45°，∴∠CFD=45°，∴FD=CD．

∵∠CDF=∠ADB=90°，∴∠CDA=∠FDB．

在△ADC和△BDF中，∵CD=DF，∠CDA=∠FDB，AD=DB，∴△ADC≌△BDF，∴∠ACD=∠BFD=45°，AC=BF．

∵∠CFD=45°，∴∠BFC=90°，∴BF⊥AC，∴S△ABC=ACBF=×5×5=．故答案为：．