ĖâÄŋÄÚČÝ
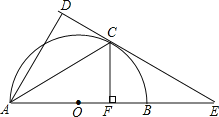
ĄūĖâÄŋĄŋĢĻąūĖâÂú·Ö10·ÖĢĐČįÍžĢŽÖąÏßy=Đ![]() x+6·ÖąðÓëxÖáĄĒyÖá―ŧÓÚAĄĒBÁ―ĩãĢŧÖąÏßy=
x+6·ÖąðÓëxÖáĄĒyÖá―ŧÓÚAĄĒBÁ―ĩãĢŧÖąÏßy=![]() xÓëAB―ŧÓÚĩãCĢŽÓëđýĩãAĮŌÆ―ÐÐÓÚyÖáĩÄÖąÏß―ŧÓÚĩãDĢŪĩãEīÓĩãAģö·ĒĢŽŌÔÃŋÃë1ļöĩĨÎŧĩÄËŲķČŅØxÖáÏōŨóÔËķŊĢŪđýĩãEŨũxÖáĩÄīđÏßĢŽ·Öąð―ŧÖąÏßABĄĒODÓÚPĄĒQÁ―ĩãĢŽŌÔPQΊąßÏōÓŌŨũÕý·―ÐÎPQMNĢŪÉčÕý·―ÐÎPQMNÓëĄũACDÖØĩþēŋ·ÖĢĻŌõÓ°ēŋ·ÖĢĐĩÄÃæŧýΊSĢĻÆ―·―ĩĨÎŧĢĐĢŽĩãEĩÄÔËķŊĘąžäΊtĢĻÃëĢĐĢŪ
xÓëAB―ŧÓÚĩãCĢŽÓëđýĩãAĮŌÆ―ÐÐÓÚyÖáĩÄÖąÏß―ŧÓÚĩãDĢŪĩãEīÓĩãAģö·ĒĢŽŌÔÃŋÃë1ļöĩĨÎŧĩÄËŲķČŅØxÖáÏōŨóÔËķŊĢŪđýĩãEŨũxÖáĩÄīđÏßĢŽ·Öąð―ŧÖąÏßABĄĒODÓÚPĄĒQÁ―ĩãĢŽŌÔPQΊąßÏōÓŌŨũÕý·―ÐÎPQMNĢŪÉčÕý·―ÐÎPQMNÓëĄũACDÖØĩþēŋ·ÖĢĻŌõÓ°ēŋ·ÖĢĐĩÄÃæŧýΊSĢĻÆ―·―ĩĨÎŧĢĐĢŽĩãEĩÄÔËķŊĘąžäΊtĢĻÃëĢĐĢŪ

ĢĻ1ĢĐĮóĩãCĩÄŨøąęĢŪ
ĢĻ2ĢĐĩą0ĢžtĢž5ĘąĢŽĮóSÓëtÖŪžäĩÄšŊĘýđØÏĩĘ―ĢŽēĒĮóSĩÄŨîīóÖĩĄĢ
ĢĻ3ĢĐĩątĢū0ĘąĢŽÖą―ÓÐīģöĩãĢĻ5ĢŽ3ĢĐÔÚÕý·―ÐÎPQMNÄÚēŋĘątĩÄČĄÖĩ·ķΧĄĢ
Ąūīð°ļĄŋĢĻ1ĢĐCĢĻ3ĢŽ![]() ĢĐĢŧĢĻ2ĢĐS=4t2Đ40t+100ĢŽSŨîīó=
ĢĐĢŧĢĻ2ĢĐS=4t2Đ40t+100ĢŽSŨîīó=![]() ĄĪĢĻ3ĢĐ3ĢžtĢž4 ŧō tĢū7
ĄĪĢĻ3ĢĐ3ĢžtĢž4 ŧō tĢū7
Ąū―âÎöĄŋĘÔĖâ·ÖÎöĢšĢĻ1ĢĐ―ây=Đ![]() x+6Óëy=
x+6Óëy=![]() xÁŠÁĒĩÄ·―ģĖŨéžīŋÉĢŧ
xÁŠÁĒĩÄ·―ģĖŨéžīŋÉĢŧ
ĢĻ2ĢĐ·ÖąðĮóģö0ĢžtĄÜ![]() ĘąšÍ
ĘąšÍ![]() ĄÜtĢž5ĘąĩÄSÓëtÖŪžäĩÄšŊĘýđØÏĩĘ―ĢŽČŧšóĀûÓÃķþīΚŊĘýĩÄÐÔÖĘĮóģöŨîīóÖĩĢŽąČ―ÏČĄīóĩÄĢŧĢĻ3ĢĐĩãĢĻ5ĢŽ3ĢĐÔÚÕý·―ÐÎPQMNÄÚēŋĘąĢŽĩãEÔÚxÖáÉÏÔËķŊĢŽ·ÖĮéŋöĖÖÂÛĢŪ
ĄÜtĢž5ĘąĩÄSÓëtÖŪžäĩÄšŊĘýđØÏĩĘ―ĢŽČŧšóĀûÓÃķþīΚŊĘýĩÄÐÔÖĘĮóģöŨîīóÖĩĢŽąČ―ÏČĄīóĩÄĢŧĢĻ3ĢĐĩãĢĻ5ĢŽ3ĢĐÔÚÕý·―ÐÎPQMNÄÚēŋĘąĢŽĩãEÔÚxÖáÉÏÔËķŊĢŽ·ÖĮéŋöĖÖÂÛĢŪ
ĘÔĖâ―âÎöĢšĢĻ1ĢĐĄßÖąÏßy=Đ![]() x+6ÓëÖąÏßy=
x+6ÓëÖąÏßy=![]() x―ŧÓÚĩãCĢŽ
x―ŧÓÚĩãCĢŽ
Ąā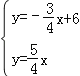 ĢŽ―âĩÃ
ĢŽ―âĩÃ![]() ĢŽ
ĢŽ
ĄāCĢĻ3ĢŽ![]() ĢĐĢŧ
ĢĐĢŧ
ĢĻ2ĢĐĄßAĩãŨøąęΊĢĻ8ĢŽ0ĢĐĢŽ
ļųūÝĖâŌâĢŽĩÃAE=tĢŽOE=8Đt
ĄāĩãQĩÄŨÝŨøąęΊ![]() ĢĻ8ĐtĢĐĢŽĩãPĩÄŨÝŨøąęΊ
ĢĻ8ĐtĢĐĢŽĩãPĩÄŨÝŨøąęΊ![]() tĢŽ
tĢŽ
ĄāPQ=![]() ĢĻ8ĐtĢĐĐ
ĢĻ8ĐtĢĐĐ![]() t=10Đ2tĢŪ
t=10Đ2tĢŪ
ĩą0ĢžtĄÜ![]() ĘąĢŽS=tĢĻ10Đ2tĢĐĢŽžīS=Đ2t2+10tĢŪĩąt=
ĘąĢŽS=tĢĻ10Đ2tĢĐĢŽžīS=Đ2t2+10tĢŪĩąt=![]() ĘąĢŽSŨîīó=
ĘąĢŽSŨîīó=![]()
ĩą![]() ĄÜtĢž5ĘąĢŽS=ĢĻ10Đ2tĢĐ2ĢŽžīS=4t2Đ40t+100ĢŪĩąt=
ĄÜtĢž5ĘąĢŽS=ĢĻ10Đ2tĢĐ2ĢŽžīS=4t2Đ40t+100ĢŪĩąt=![]() ĘąĢŽSŨîīó=
ĘąĢŽSŨîīó=![]()
Ąß![]() Ģū
Ģū![]() ĢŽ ĄāSŨîīó=
ĢŽ ĄāSŨîīó=![]()
ĢĻ3ĢĐ3ĢžtĢž4 ŧō tĢū7

ĄūĖâÄŋĄŋÄģđĪģ§ÉúēúēŋÃÅΊÁË―âąūēŋÃÅđĪČËĩÄÉúēúÄÜÁĶĮéŋöĢŽ―øÐÐÁËģéŅųĩũēéĢŪļÃēŋÃÅËæŧúģéČĄÁË30ÃûđĪČËÄģĖėÃŋČËžÓđĪÁãžþĩÄļöĘýĢŽĘýūÝČįÏÂĢš
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
ÕûĀíÉÏÃæĘýūÝĢŽĩÃĩ―ĖõÐÎÍģžÆÍžĢš
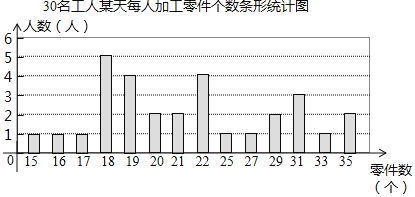
ŅųąūĘýūÝĩÄÆ―ūųĘýĄĒÖÚĘýĄĒÖÐÎŧĘýČįÏÂąíËųĘūĢš
ÍģžÆÁŋ | Æ―ūųĘý | ÖÚĘý | ÖÐÎŧĘý |
ĘýÖĩ | 23 | m | 21 |
ļųūÝŌÔÉÏÐÅÏĒĢŽ―âīðÏÂÁÐÎĘĖâĢš
ĢĻ1ĢĐÉÏąíÖÐÖÚĘýmĩÄÖĩΊĄĄ ĄĄĢŧ
ĢĻ2ĢĐΊĩũķŊđĪČËĩÄŧýžŦÐÔĢŽļÃēŋÃÅļųūÝđĪČËÃŋĖėžÓđĪÁãžþĩÄļöĘýÖÆķĻÁË―ąĀøąęŨžĢŽ·ēīïĩ―ŧōģŽđýÕâļöąęŨžĩÄđĪČË―ŦŧņĩÃ―ąĀøĢŪČįđûÏëČÃŌŧ°ëŨóÓŌĩÄđĪČËÄÜŧņ―ąĢŽÓĶļųūÝĄĄ ĄĄĀīČ·ķĻ―ąĀøąęŨžąČ―ÏšÏĘĘĢŪĢĻĖîĄ°Æ―ūųĘýĄąĄĒĄ°ÖÚĘýĄąŧōĄ°ÖÐÎŧĘýĄąĢĐ
ĢĻ3ĢĐļÃēŋÃÅđæķĻĢšÃŋĖėžÓđĪÁãžþĩÄļöĘýīïĩ―ŧōģŽđý25ļöĩÄđĪČËΊÉúēúÄÜĘÖĢŪČôļÃēŋÃÅÓÐ300ÃûđĪČËĢŽĘÔđĀžÆļÃēŋÃÅÉúēúÄÜĘÖĩÄČËĘýĢŪ