Question

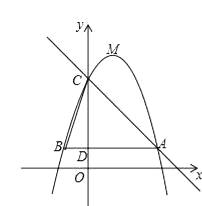
【题目】如图，已知二次函数y=﹣x2+bx+c（b，c为常数）的图象经过点A（5，3），点C（0，8），顶点为点M，过点A作AB∥x轴，交y轴于点D，交该二次函数图象于点B，连结BC．

（1）求该二次函数的解析式及点M的坐标；

（2）求△ABC的面积；

（3）若将该二次函数图象向下平移m（m＞0）个单位，使平移后得到的二次函数图象的顶点落在△ABC的内部（不包括△ABC的边界），求m的取值范围．

Answer 1

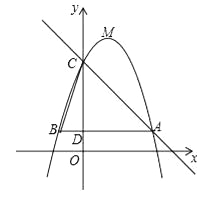
【答案】（1）y=﹣x2+4x+8，M（2，12）；（2）15；（3）6＜m＜9．

【解析】试题分析：（1）把点A、C的坐标代入函数解析式，用待定系数法求出抛物线解析式；

（2）结合点A、B、C的坐标，三角形的面积公式进行解答；

（3）点M是沿着对称轴直线x=2向下平移的，可先求出直线AC的解析式，将x=2代入求出点M在向下平移时与AC、AB相交时y的值，即可得到m的取值范围．

解：（1）把点A（5，3），点C（0，8）代入二次函数y=﹣x2+bx+c，得

，

解得，

∴二次函数解析式为y=﹣x2+4x+8，配方得y=﹣（x﹣2）2+12

∴点M的坐标为（2，12）；

（2）由（1）知，抛物线的对称轴是x=2．

∵A（5，3），AB∥x轴，

∴AB=6，D（0，3）

∵C（0，8），

∴CD=5，

∴△ABC的面积=ABCD=×6×5=15，

即△ABC的面积=15；

（3）设直线AC解析式为y=kx+b，把点A（5，3），C（0，8）代入，

解得，

∴直线AC的解析式为y=﹣x+8，对称轴直线x=2与△ABC两边分别交于点E、点F，

把x=2代入直线AC解析式y=﹣x+8，

解得y=6，则点E坐标为（2，6），点F坐标为（2，3）

∴3＜12﹣m＜6，解得6＜m＜9．