题目内容
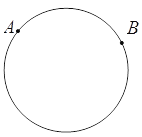
【题目】如图,已知一周长为30cm的圆形轨道上有相距10cm的A、B两点 (备注:圆形轨道上两点的距离是指圆上这两点间较短部分展直后的线段长).动点P从A点出发,以a cm/s的速度,在轨道上按逆时针方向运动,与此同时,动点Q从B出发,以3 cm/s的速度,按同样的方向运动.设运动时间为t (s),当t = 5时,动点P、Q第一次相遇.
(1)求a的值;
(2)若a > 3,在P、Q第二次相遇前,当动点P、Q在轨道上相距12cm时,求t的值.
【答案】(1)a=1或a=7;(2)t的值为0.5、2、8或9.5.
【解析】试题分析:(1)根据相遇时,点P和点Q的运动的路程和等于AB的长列方程即可求解;
(2)设经过ts,P、Q两点相距12cm,分相遇前和相遇后两种情况建立方程求出其解;分点P,Q只能在直线AB上相遇,而点P旋转到直线AB上的时间分两种情况,所以根据题意列出方程分别求解.
试题解析:(1)若a<3,则3×5-5a=10,解得:a=1;
若a>3,则5a-3×5=20,解得:a=7;
(2)∵a>3,∴a=7,共有4种可能:
①7t+10-3t=12,解得:t=0.5;
②7t+10-3t=18,解得:t=2;
③7t+10-3t=42,解得:t=8;
④7t+10-3t=48,解得:t=9.5;
综上所知,t的值为0.5、2、8或9.5.

练习册系列答案
相关题目