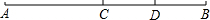题目内容
 如图,D是线段AB、BC垂直平分线的交点,若∠ABC=150°,则∠ADC的大小是
如图,D是线段AB、BC垂直平分线的交点,若∠ABC=150°,则∠ADC的大小是
- A.60°
- B.70°
- C.75°
- D.80°
A
分析:连接BD.根据线段垂直平分线的性质,得AD=BD=CD,根据等边对等角,得∠A=∠ABD,∠C=∠CBD.根据∠ABC=150°和四边形的内角和定理,即可求得∠ADC的度数.
解答: 解:连接BD.
解:连接BD.
∵D是线段AB、BC垂直平分线的交点,
∴AD=BD,BD=CD.
∴∠A=∠ABD,∠C=∠CBD.
又∠ABC=150°,
∴∠ADC=360°-150°×2=60°.
故选A.
点评:此题考查了线段垂直平分线的性质、等边对等角的性质和四边形的内角和定理.正确作出辅助线是解答本题的关键.
分析:连接BD.根据线段垂直平分线的性质,得AD=BD=CD,根据等边对等角,得∠A=∠ABD,∠C=∠CBD.根据∠ABC=150°和四边形的内角和定理,即可求得∠ADC的度数.
解答:
 解:连接BD.
解:连接BD.∵D是线段AB、BC垂直平分线的交点,
∴AD=BD,BD=CD.
∴∠A=∠ABD,∠C=∠CBD.
又∠ABC=150°,
∴∠ADC=360°-150°×2=60°.
故选A.
点评:此题考查了线段垂直平分线的性质、等边对等角的性质和四边形的内角和定理.正确作出辅助线是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,C是线段AB的中点,D是线段CB上一点,下列说法错误的是( )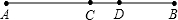
| A、CD=AC-BD | ||
| B、CD=AD-BC | ||
C、CD=
| ||
D、CD=
|
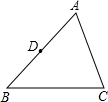 如图,D是线段AB的中点,在图中过D画出BC平行线,交AC于E,并量一量线段AE和EC的长,你得到什么结论?量一量线段DE和BC的长,你又能得到什么结论?
如图,D是线段AB的中点,在图中过D画出BC平行线,交AC于E,并量一量线段AE和EC的长,你得到什么结论?量一量线段DE和BC的长,你又能得到什么结论? 、BE.
、BE. 如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.