题目内容
已知，如图，D是线段AB上的点，以BD为直径作⊙O，AP切⊙O于E，BC⊥AF于C，连接DE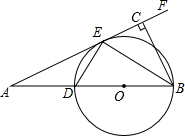
、BE．（1）求证：BE平分∠ABC；
（2）若D是AB中点，⊙O直径BD=3
| 3 |
分析：（1）可利用CE是圆的切线来求证，连接OE，因此OE∥BC（都和AF垂直），可根据内错角相等和等边对等角，将相等角进行替换即可得出∠EBD=∠EBC．
（2）可通过构建直角三角形来求解．过E作EH⊥AB于H，那么不难得出EDH和BDE相似，可得出DE2=DH•DB，那么求出DH就是关键，也就是求出BH的长．根据（1）的角平分线，我们不难得出BH=BC，那么就必须求出BC，有AB的长，只要知道∠A的正弦值就可以求出BC了，在直角三角形AOE中，AO=3OE，由此可得出∠A的正弦值，也就求出BC、BH、DH的长了，然后可根据上面上面所述的步骤求出DE的长．
（2）可通过构建直角三角形来求解．过E作EH⊥AB于H，那么不难得出EDH和BDE相似，可得出DE2=DH•DB，那么求出DH就是关键，也就是求出BH的长．根据（1）的角平分线，我们不难得出BH=BC，那么就必须求出BC，有AB的长，只要知道∠A的正弦值就可以求出BC了，在直角三角形AOE中，AO=3OE，由此可得出∠A的正弦值，也就求出BC、BH、DH的长了，然后可根据上面上面所述的步骤求出DE的长．
解答：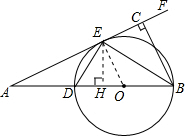
（1）证明：连接OE，
∵AF与⊙O切于点E，
∴OE⊥AC．
又BC⊥AF于C，
∴OE∥BC．
∴∠OEB=∠EBC，
∵OB=OE，
∴∠OEB=∠OBE，
∴∠OBE=∠EBC，
∴BE平分∠ABC．
（2）解：过E作EH⊥AB于H，连接OE，
在直角三角形OEA中，sinA=OE：AO=OE：3OE=1：3，
直角三角形ABC中，AB=2BD=6
，
BC=AB•sinA=6×
=2
，
∵∠EHB=∠ECB=90°，BE=BE，∠EBA=∠EBC，
∴△EBH≌△ECB．
∴BH=BC=2
．
∴DH=
．
∵∠DEB=∠EHD=90°，∠EDO=∠BDE，
∴△EDH∽△BDE．
∴DE2=DH•DB=
×3
=9．
∴DE=3．
（1）证明：连接OE，∵AF与⊙O切于点E，
∴OE⊥AC．
又BC⊥AF于C，
∴OE∥BC．
∴∠OEB=∠EBC，
∵OB=OE，
∴∠OEB=∠OBE，
∴∠OBE=∠EBC，
∴BE平分∠ABC．
（2）解：过E作EH⊥AB于H，连接OE，
在直角三角形OEA中，sinA=OE：AO=OE：3OE=1：3，
直角三角形ABC中，AB=2BD=6
| 3 |
BC=AB•sinA=6×
| 1 |
| 3 |
| 3 |
∵∠EHB=∠ECB=90°，BE=BE，∠EBA=∠EBC，
∴△EBH≌△ECB．
∴BH=BC=2
| 3 |
∴DH=
| 3 |
∵∠DEB=∠EHD=90°，∠EDO=∠BDE，
∴△EDH∽△BDE．
∴DE2=DH•DB=
| 3 |
| 3 |
∴DE=3．
点评：本题考查了切线的性质，解直角三角形等知识点，通过切线的性质得出角相等或垂直是解题的关键．
练习册系列答案
相关题目
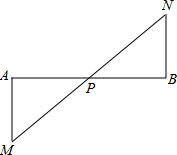（2012•北京二模）已知：如图，P是线段AB的中点，线段MN经过点P，MA⊥AB，NB⊥AB．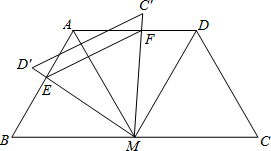
已知：如图，C是线段AB的中点，∠A=∠B，∠ACE=∠BCD．