题目内容
如图,C是线段AB的中点,D为线段CB的中点,BD=1.2cm,求AD的长.

分析:根据线段中点得出AC=BC,CD=BD=
BC,求出CD、求出AC、BC,即可求出答案.
| 1 |
| 2 |
解答:解:∵C是线段AB的中点,
∴AC=BC,
∵D是线段CB的中点,BD=1.2cm,
∴CD=BD=
BC=1.2cm,
∴BC=2.4cm,
∴AC=BC=2.4cm,
∴AD=AC+CD=2.4cm+1.2cm=3.6cm;
答:AD的长是3.6cm.
∴AC=BC,
∵D是线段CB的中点,BD=1.2cm,
∴CD=BD=
| 1 |
| 2 |
∴BC=2.4cm,
∴AC=BC=2.4cm,
∴AD=AC+CD=2.4cm+1.2cm=3.6cm;
答:AD的长是3.6cm.
点评:本题考查了两点间的距离,用到的知识点是线段的中点,关键是根据中点和已知条件求出AC,CD的长.

练习册系列答案
相关题目
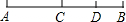 如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )
如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )| A、CD=AC-BD | ||
B、CD=
| ||
C、CD=
| ||
| D、CD=AD-BC |
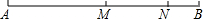
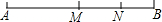 如图,M是线段AB的中点,N是线段MB的中点,且NB=6,求AB的长.
如图,M是线段AB的中点,N是线段MB的中点,且NB=6,求AB的长.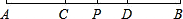 如图,P是线段AB的中点,点C、D把线段AB三等份.已知线段CP的长为2cm,求线段AB的长.
如图,P是线段AB的中点,点C、D把线段AB三等份.已知线段CP的长为2cm,求线段AB的长.